Rect¨¢ngulos singulares

Hemos visto, en las semanas anteriores, algunas de las posibilidades del rect¨¢ngulo de 2 x 1 como tesela, tatami o ladrillo, que lo convierten, seguramente, en el m¨¢s ¡°popular¡± y difundido de los rect¨¢ngulos. Pero hay al menos otros dos rect¨¢ngulos especiales que encontramos a menudo a nuestro alrededor.

Uno de ellos es el folio DIN A4 (la expresi¨®n no es del todo correcta, pues el folio propiamente dicho es una hoja de 215 x 315 mil¨ªmetros, algo mayor que el DIN A4 y actualmente en desuso). Seguro que tienes a mano uno de estos folios homologados. ?Qu¨¦ pasa si lo doblas por la mitad? Y viendo lo que pasa al doblarlo y sabiendo que su lado menor mide 21 cm, ?cu¨¢nto mide el lado mayor? (No se trata de coger una regla y medirlo, sino de deducirlo).

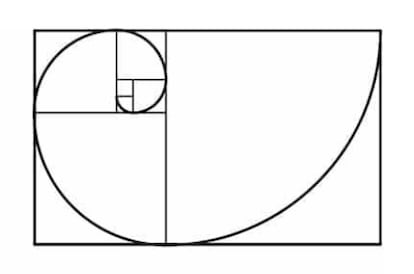
Pero el m¨¢s notable, si no el m¨¢s popular, de los rect¨¢ngulos es el que cumple la propiedad que ilustra la figura adjunta: si a partir de un v¨¦rtice llevamos el lado menor sobre el mayor y, levantando una perpendicular desde su extremo, formamos un cuadrado, el rect¨¢ngulo menor resultante es proporcional al rect¨¢ngulo mayor. Si el lado menor mide 1, ?cu¨¢nto mide el mayor?

Es el famoso rect¨¢ngulo ¨¢ureo o rect¨¢ngulo dorado, que ya los antiguos griegos tomaron como referente est¨¦tico para sus construcciones y obras de arte (lo encontramos, por ejemplo, en la fachada del Parten¨®n). Los arquitectos y artistas pl¨¢sticos del Renacimiento lo recuperaron y utilizaron profusamente (es f¨¢cil descubrirlo, por ejemplo, en las composiciones pict¨®ricas de Leonardo), y sigue siendo un referente est¨¦tico imprescindible en la actualidad. Tambi¨¦n en la fachada de la catedral de Notre Dame, que hace exactamente un a?o sufri¨® un terrible incendio, encontramos varios rect¨¢ngulos dorados, ?los distingues?

?Podr¨ªas construir un rect¨¢ngulo ¨¢ureo con regla (no graduada) y comp¨¢s?

Pero ?por qu¨¦ precisamente esta proporci¨®n nos parece tan bella? La relaci¨®n entre los lados del rect¨¢ngulo ¨¢ureo no es un n¨²mero entero, ni siquiera racional, por lo que los pitag¨®ricos se resistieron a aceptar este modelo. Y sin embargo se impuso, y para siempre. ?D¨®nde reside su rec¨®ndita armon¨ªa?

Puesto que el rect¨¢ngulo menor de la figura anterior es semejante al mayor, tambi¨¦n es ¨¢ureo, y podemos repetir con ¨¦l la operaci¨®n, y tambi¨¦n con el siguiente, y as¨ª sucesiva e indefinidamente. Y si en cada uno de los sucesivos cuadrados resultantes trazamos un cuadrante de circunferencia, obtenemos una espiral dorada, tambi¨¦n conocida como espiral de Durero, que es una buena aproximaci¨®n a un espiral equiangular (aquella en la que el ¨¢ngulo que forman el radio vector y la tangente es constante).

Y del cuadrado duplicado del rect¨¢ngulo de 2 x 1, a un fantasmal cuadrado demediado: el de la figura adjunta, enviada por Carlos Gaceo.

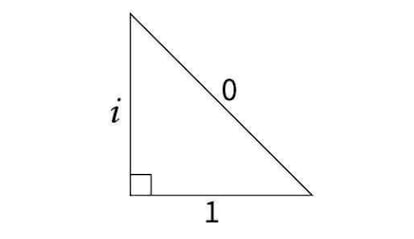
Por el teorema de Pit¨¢goras, i al cuadrado + 1 al cuadrado = -1 + 1 = 0. ?Qu¨¦ puedes decir al respecto?

Y, por ¨²ltimo, en nuestra relaci¨®n de rect¨¢ngulos singulares falta uno, ?cu¨¢l es?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos Maldita f¨ªsica, Malditas matem¨¢ticas o El gran juego. Fue guionista de La bola de cristal.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter.