?Todo n¨²mero entero es la suma de, como mucho, nueve cubos?

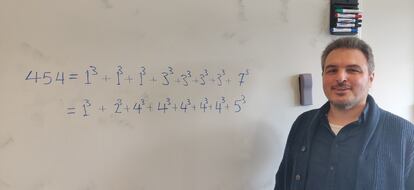
Si tratamos de expresar un n¨²mero entero como suma de cubos de enteros, ?cu¨¢ntos necesitamos? Para algunos hace falta solo uno, por ejemplo 8 = 2?, pero para otros hacen falta hasta nueve sumandos (por ejemplo, 23 = 2? + 2? + 1? + 1? + 1? + 1? + 1? + 1? + 1?, y no hay otra forma m¨¢s sencilla de expresarlo). ?Es posible que algunos necesiten 10, 20, 200...? O, ?es nueve el menor n¨²mero de sumandos con los que se puede escribir cualquier n¨²mero como suma de cubos? As¨ª lo conjetur¨® en 1770 el ingl¨¦s Edward Waring.

A lo largo de la historia estos problemas se estudiaban mediante el uso de computadoras humanas. Eran prodigios en el c¨¢lculo mental, no necesariamente matem¨¢ticos, que se encargaban de elaborar largas tablas de n¨²meros manualmente. Uno de ellos fue Zacharias Dase, que en la mitad del siglo XIX obtuvo los primeros 200 d¨ªgitos del n¨²mero pi. Tambi¨¦n estudi¨® el problema de la suma de cubos, prestando su ayuda al c¨¦lebre matem¨¢tico Carl Jacobi.

Jacobi hab¨ªa observado que si al dividir cualquier n¨²mero por 9 se tiene como resto 4 o 5 (lo que sucede para infinitos n¨²meros enteros), entonces no se puede expresar como suma de tres cubos (positivos o negativos). Por tanto, podemos afirmar que como m¨ªnimo se necesitar¨¢n cuatro cubos para expresar cualquier n¨²mero. Jacobi propuso a Dase construir una tabla de la expresi¨®n como suma del m¨ªnimo n¨²mero de cubos positivos para todos los n¨²meros menores que 12000. As¨ª comprobaron que para todos los n¨²meros de la tabla la afirmaci¨®n de Waring era cierta. Si hubieran encontrado tan solo uno que no verificase la propiedad, el problema ya estar¨ªa resuelto. Sin embargo, comprobando que era cierto para 12000 no (?a¨²n quedar¨ªan infinitos n¨²meros por verificar!). Pese a ello esta constataci¨®n, junto con otros argumentos, fue clave en la resoluci¨®n de la conjetura.

Adem¨¢s, observaron que todos los n¨²meros de la tabla excepto el 23 y el 239 pod¨ªan expresarse como suma de ocho cubos; y excepto el 15, 22, 23, 50, 114, 167, 175, 186, 212, 231, 238, 239, 303, 364, 420, 428, 454, como la suma de siete cubos; adem¨¢s solo 138 enteros positivos necesitaban seis cubos, siendo el mayor de ellos 8042. Con estas observaciones, Jacobi conjetur¨® que, salvo un n¨²mero finito de enteros, cualquier n¨²mero era la suma de cinco cubos.

Hubo que esperar hasta el siglo XX para obtener avances en estos problemas. Entre 1908 y 1912 Arthur Wieferich y Alfred Kemper demostraron la afirmaci¨®n de Waring. En concreto, probaron que todo entero mayor que 2,25 ¡¤ (10^9) era suma de nueve cubos, y para todos los enteros menores utilizaron las tablas de R.D. von Sterneck, que ampliaban las de Dase hasta 40 000. En 1908 Edmund Landau demostr¨® que cualquier entero era la suma de ocho cubos, salvo una cantidad finita de ellos. En 1938, Leonard Dickson prob¨® que solo 23 y el 239 necesitan nueve cubos. Para ello necesit¨® la ayuda de su asistente, Evelyn Garbe, que extendi¨® en cuatro semanas las tablas de von Sterneck hasta 123 000.

A¨²n queda abierto "uno de los m¨¢s profundos misterios de la aritm¨¦tica¡±, seg¨²n G.H. Hardy

Posteriormente se fueron consiguiendo cotas para el menor entero que puede no ser la suma de siete cubos: Kevin McCurley prob¨® que era un n¨²mero menor que 10^500000y Olivier Ramar¨¦, en 2007, que ten¨ªa que ser menor que 3,72 ¡¤ (10^227). A la vista de tales cifras, no parec¨ªa viable comprobar todos los casos menores a la cota, uno a uno, ni con la ayuda de supercomputadoras. En 2010, nuevas ideas de Kent Bocklan y Noam Elkies permitieron resolver el caso par y recientemente, gracias al trabajo de Samir Siksek, se ha solucionado el caso impar. Estos resultados han requerido potentes ordenadores (el caso impar necesit¨® cerca de tres semanas de c¨¢lculo intensivo en 59 procesadores) para completar la prueba de que todos los n¨²meros excepto el 15, 22, 23, 50, 114, 167, 175, 186, 212, 231, 238, 239, 303, 364, 420, 428, 454 son la suma de, como mucho, siete cubos.

Pero este tour de force a¨²n no ha acabado. Resultados computacionales y heur¨ªsticos han permitido conjeturar que el mayor entero que no se puede poner como suma de seis cubos es 8042 (con 138 excepciones); como suma de cinco cubos es 1290740 (con 4060 excepciones), o como suma de cuatro cubos es 7373170279850 (con 113936676 excepciones), por el momento no hay resultados te¨®ricos que determinen que cualquier n¨²mero natural, salvo un n¨²mero finito de ellos, sea la suma de a lo m¨¢s seis, cinco o cuatro cubos positivos (recordemos que para tres hay infinitas excepciones). As¨ª que a¨²n queda abierto ¡°uno de los m¨¢s profundos misterios de la aritm¨¦tica¡±, como denomin¨® G.H. Hardy en 1920 a esta cuesti¨®n.

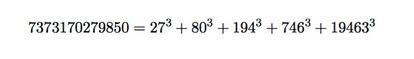
Enrique Gonz¨¢lez Jim¨¦nez es profesor de la Universidad Aut¨®noma de Madrid

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n Garc¨ªa-Longoria (ICMAT)

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter