Aut¨®matas celulares

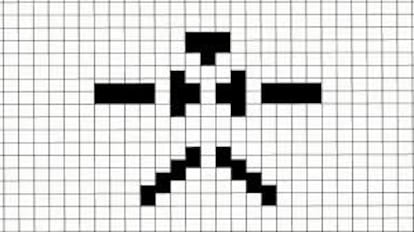
El comportamiento de la hormiga de Langton, a la que dedicamos el art¨ªculo anterior, en una cuadr¨ªcula con todas las casillas en blanco como situaci¨®n de partida, es muy peculiar. Al principio forma patrones sencillos, pero tras unos cientos de movimientos aparece una gran estructura compacta y de aspecto desordenado, como se puede ver en la ilustraci¨®n de la semana pasada. Y lo m¨¢s sorprendente es que luego, a partir de los diez mil movimientos, aparece una ¡°avenida¡± en alguna de las direcciones diagonales (NE, NO, SE o SO), generada por una secuencia de 104 pasos que se repite indefinidamente.

Al parecer, y aunque a¨²n no se ha podido demostrar de forma concluyente, sea cual fuere la configuraci¨®n de partida la hormiga acaba generando una de estas avenidas infinitas (conjetura de Cohen-Kong). Lo que s¨ª se ha demostrado, contestando a una de las preguntas de la semana pasada, es que el ¡°hormiguero¡± generado por la hormiga siempre crece indefinidamente, sea cual fuere la configuraci¨®n de partida (la demostraci¨®n, dada por el teorema de Bunimovitch-Troubetzkoy, es sencilla pero farragosa, y se encuentra f¨¢cilmente en la red).

La hormiga confinada y la hormiga 3D

?Y si la hormiga de Langton se moviera en una cuadr¨ªcula finita?

Imaginemos una hormiga en una de las casillas centrales de un tablero de ajedrez como posici¨®n de partida. Cuando topa con un borde, la hormiga ¡°rebota¡± y queda en la misma casilla, pero con la flecha apuntando en direcci¨®n contraria; ?qu¨¦ configuraci¨®n obtendr¨ªamos despu¨¦s de n movimientos? Y si en vez de ¡°rebotar la hormiga sale por el otro lado, es decir, pasa al otro extremo de la misma fila o columna, como si saliera del borde opuesto, ?qu¨¦ pasar¨ªa en este caso?

Tambi¨¦n podemos sustituir la cuadr¨ªcula por una ¡°cub¨ªcula¡±, una red tridimensional de celdillas c¨²bicas; pero para que la hormiga pueda desplazarse tambi¨¦n en vertical, tenemos que modificar las reglas. ?De qu¨¦ manera podemos hacerlo?

Otros aut¨®matas

La hormiga de Langton y sus variantes, as¨ª como los distintos patrones del juego de la vida (osciladores, vidas est¨¢ticas, naves espaciales, etc.) y el juego en s¨ª mismo son ¡°aut¨®matas celulares¡±, objetos matem¨¢ticos y computacionales que no es f¨¢cil definir en pocas palabras, aunque s¨ª visualizarlos. En general, el aut¨®mata celular tiene como base una cuadr¨ªcula (aunque tambi¨¦n puede ser una rejilla hexagonal, triangular, etc.) cuyas celdillas -las ¡°c¨¦lulas¡±- pueden hallarse en distintos estados (generalmente dos), que var¨ªan de acuerdo con unas reglas sencillas.

Por ejemplo, en el caso del juego de la vida, como vimos, cada c¨¦lula puede hallarse en dos estados, ¡°viva¡± o ¡°muerta¡±, y ese estado depende de las c¨¦lulas vecinas, que pueden mantenerla viva, resucitarla o matarla, ya sea por soledad o por superpoblaci¨®n.

Invito a mis sagaces lectores a inventar sus propios aut¨®matas celulares, o a introducir alguna variante en los ya existentes. Solo hace falta una hoja de papel cuadriculado y un poco de imaginaci¨®n (aunque un buen programa inform¨¢tico puede ser de gran ayuda).

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter