La hormiga de Langton

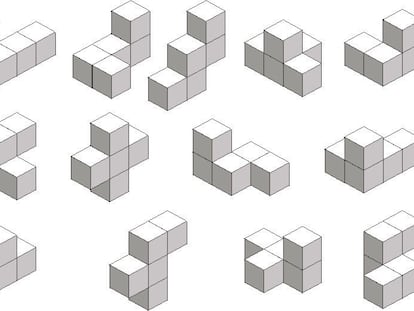
En respuesta a lo planteado la semana pasada, solo 3 de los 8 tetracubos no pueden obtenerse por ¡°engrosamiento¡± de alg¨²n tetromin¨® (y un par de ellos son sim¨¦tricos especulares, como se ve en la figura).

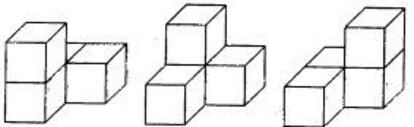
Sin embargo, basta con echar una ojeada a la ilustraci¨®n de la semana pasada para ver que entre los pentacubos la situaci¨®n se invierte: solo 3 de los 13 pentacubos son versiones tridimensionales de sendos pentomin¨®s (F, W y X).

Con 9 tricubos I se puede formar un cubo de 3 x 3 x 3 de tres maneras distintas (ver comentario 75 de Policubos).

Con 9 tricubos V tambi¨¦n se puede, en principio, formar un cubo de 3 x 3 x 3, como se puede ver aplicando un criterio de paridad similar al utilizado en semanas anteriores para resolver problemas an¨¢logos en dos dimensiones. En efecto, si coloreamos los 27 cubitos unitarios de un cubo de 3 x 3 x 3 alternativamente en blanco y negro, como si fuera un damero tridimensional, tendremos 13 cubitos de un color y 14 de otro, pongamos 13 blancos y 14 negros. Si en 5 de los 9 tricubos V coloreamos 2 cubitos de negro y 1 (el central) de blanco, y en los otros 4 tricubos coloreamos dos cubitos de blanco y uno de negro, tendremos 2 x 5 + 4 = 14 cubitos negros y 5 + 2 x 4 = 13 cubitos blancos alternantes, luego la construcci¨®n es posible.

Se hace hormiguero al andar

Hemos visto en las ¨²ltimas semanas, al hablar de los poliomin¨®s y del juego de la vida, cu¨¢nto da de s¨ª una cuadr¨ªcula, sea un tablero de ajedrez o una hoja de papel cuadriculado, y ya sea como espacio a recubrir o como escenario de las andanzas de aut¨®matas celulares como los de Conway.

El gran ¨¦xito del juego de la vida estimul¨® la creaci¨®n de otros aut¨®matas similares, y uno de los m¨¢s interesantes es la hormiga de Langton, inventada por el cient¨ªfico inform¨¢tico estadounidense Christopher Langton en 1986.

La hormiga de Langton se mueve en una cuadr¨ªcula en la que cada casilla puede estar en uno de dos estados: blanco o negro, 1 o 0, ¡°viva¡± o ¡°muerta¡±, encendida o apagada, etc.

Una forma sencilla de ¡°poner en marcha¡± la hormiga de Langton es la siguiente: en una hoja de papel cuadriculado se marcan algunas casillas al azar con l¨¢piz (no con bol¨ªgrafo, pues las marcas se han de poder borrar) y luego, tambi¨¦n al azar se sit¨²a en una de las casillas la ¡°hormiga¡±, que es una flechita que apunta hacia uno de los cuatro lados del cuadradito que la contiene: norte, sur, este u oeste. La hormiga opera de acuerdo con las siguientes reglas:

Si est¨¢ en una casilla blanca, cambia el color de la casilla, gira noventa grados a la izquierda y avanza una casilla.

Si est¨¢ en una casilla negra, cambia el color de la casilla, gira noventa grados a la derecha y avanza una casilla.

Imaginemos la situaci¨®n inicial m¨¢s simple: la hormiga en medio de una cuadr¨ªcula con todas las casillas blancas. ?Qu¨¦ ocurrir¨¢? ?Aumentar¨¢ indefinidamente el n¨²mero de casillas negras o alcanzar¨¢ un m¨¢ximo insuperable?

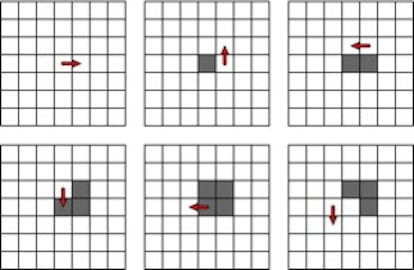
Invito a mis sagaces lectoras/es a buscar situaciones de partida que den lugar a desarrollos interesantes.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter