?Entiendes realmente la cartograf¨ªa de la Tierra?

No es posible tener un sistema de coordenadas perfecto en superficies curvas. Incluso en la esfera, cualquier sistema de coordenadas que escojamos tiene sus propias peculiaridades, como podemos observar en un mapa terrestre. En esto se basa un famoso problema para ni?os sobre un cazador que coloca su tienda en un punto del planeta. Seg¨²n dice el acertijo, sale de ella y recorre 10 km estrictamente hacia al sur, 10 km al oeste, y finalmente 10 km al norte; al terminar el paseo vuelve a estar en su campamento. ?D¨®nde puede estar su tienda? En algunas versiones tambi¨¦n se menciona que el cazador vio un oso en su camino, y se pregunta sobre el color del mismo.

Como muchos lectores estar¨¢n pensando, una soluci¨®n es el polo norte (y el color del animal ser¨¢ blanco, ya que es un oso polar). Sin embargo, ?esta soluci¨®n no es ¨²nica! Podr¨ªamos considerar un paralelo l?, de 10 km de longitud cerca del polo sur. Entonces, la tienda del cazador podr¨ªa estar en cualquier punto del c¨ªrculo de latitud m? que se encuentre a 10 km al norte del l?. Hagan el recorrido sobre la Fig.1. Ahora, en cambio, ?podr¨ªamos preguntar por el color de los ping¨¹inos con los que se encontrar¨¢ el cazador!

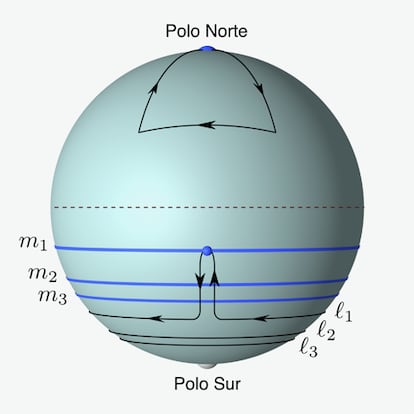
Pero aqu¨ª no acaba la cosa; tambi¨¦n en el hemisferio sur, otra soluci¨®n aparece tomando un paralelo l?, de 5 km de longitud, y luego un paralelo m? que est¨¦ a 10 km al norte de ¨¦l, y procediendo de la misma manera (en este caso, completando dos c¨ªrculos completos a lo largo del l?). En general, el cazador podr¨ªa poner su tienda en cualquier punto del n¨²mero infinito de c¨ªrculos mn, con n = 1, 2, 3, ¡­ que est¨¢n a 10 km al norte de los paralelos ln de longitud 10/n km, en las proximidades del polo sur, y completar el camino indicado.

Podemos plantearnos un problema similar, pero con un trayecto m¨¢s largo. Ahora, el cazador camina 10 km hacia el sur, luego 10 km hacia el oeste, despu¨¦s 10 km estrictamente al norte, y, finalmente, 10 km al este. Cuando termina su paseo est¨¢ de nuevo en su tienda. ?D¨®nde est¨¢ ubicada?

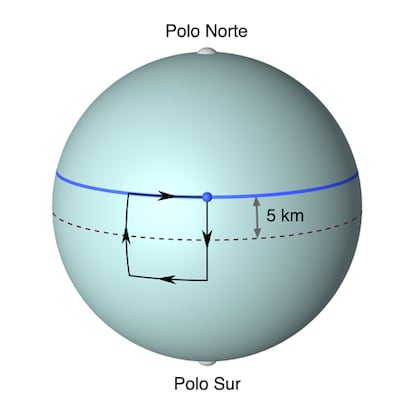
Si el cazador fuera un practicante del terraplanismo podr¨ªa comenzar en cualquier lugar, moverse a lo largo de un cuadrado plano y regresar al punto original. Pero en la Tierra el viaje se hace a lo largo de meridianos y paralelos y aunque al desplazarse al norte y al sur en los meridianos el cazador cubre los mismos segmentos, pod¨ªa perder su tienda al regresar, debido a las diferentes longitudes de las circunferencias de los paralelos cuando se desplaza al este y al oeste. Una soluci¨®n implicar¨ªa colocar la tienda en un lugar concreto en cualquier lugar del c¨ªrculo que se encuentra a 5 km al norte del ecuador, de manera que el mencionado paseo transcurra sobre dos circunferencias iguales (ver Fig.2).

Hay otras ubicaciones posibles. Modificando las soluciones obtenidas en el acertijo inicial encontramos un nuevo conjunto de caminos posibles. El trayecto del cazador tendr¨¢ una forma de ojo de cerradura (ver Fig.3). Comenzamos cerca del polo sur, en cualquier punto sobre el paralelo azul que se define por la siguiente condici¨®n. Primero viajamos hacia el sur a lo largo de un meridiano para llegar a un paralelo suficientemente corto, de modo que cuando vayamos hacia el oeste (en sentido contrario a las agujas del reloj) a lo largo del c¨ªrculo completo, y un poco m¨¢s, y luego regresemos sobre otro meridiano, llegaremos a un punto exactamente 10 km al este (en sentido horario) de la tienda. Sabemos que existe este paralelo azul gracias al teorema del valor intermedio.

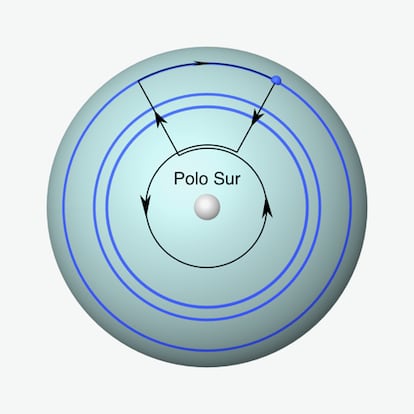
Podemos encontrar un n¨²mero infinito de soluciones similares: por ejemplo, en cualquier lugar del segundo paralelo azul, un poco m¨¢s cerca del polo sur, de modo que cuando el cazador llegue al paralelo corto de la circunferencia a un poco menos de 5 km, viaja hacia el oeste dos c¨ªrculos completos y un poco m¨¢s sobre ¨¦l, antes de regresar sobre un meridiano al segundo paralelo azul. An¨¢logamente, el cazador podr¨ªa plantar su tienda en cualquier punto del n¨²mero infinito de paralelos que tienen asociados los paralelos cortos correspondientes en las proximidades del polo sur, y satisfacen la condici¨®n anterior. Pero, adem¨¢s, como el problema es sim¨¦trico, encontramos un conjunto similar de soluciones cerca del polo norte. Y estas son todas las opciones. En ning¨²n otro lugar es posible volver a la tienda siguiendo las instrucciones indicadas.

Para terminar, volvamos a la pregunta de qu¨¦ animal tiene la posibilidad de encontrar el cazador en el camino. En los "conjuntos polares" de soluciones, la tienda est¨¢ demasiado cerca de los polos norte y sur para encontrar animales all¨ª, ya sean osos o ping¨¹inos. Sin embargo, en la soluci¨®n cuasi ecuatorial, ?el cazador podr¨ªa encontrar un ping¨¹ino de Gal¨¢pagos!

Boris Khesin es catedr¨¢tico de Matem¨¢ticas en la Universidad de Toronto (Canad¨¢)

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Traducci¨®n, edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n Garc¨ªa-Longoria (ICMAT)

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter