Pent¨¢gonos y hex¨¢gonos

Como hemos visto en las ¨²ltimas semanas, la secuencia de los n¨²meros triangulares es 1, 3, 6, 10, 15, 21¡­, y la de los cuadrados, 1, 4, 9, 16, 25, 36¡­ ?Cu¨¢l ser¨¢ la secuencia de los n¨²meros pentagonales?

Conviene empezar se?alando que, a diferencia de los n¨²meros triangulares y cuadrados, los n¨²meros pentagonales se forman seg¨²n patrones de contorno.

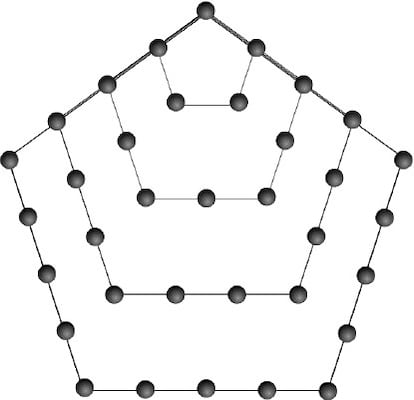
Para hallar, por ejemplo, el quinto n¨²mero pentagonal, empezamos formando un pent¨¢gono regular de 5 puntos de lado, y luego a partir de uno de los v¨¦rtices, vamos formando sucesivos pent¨¢gonos de puntos con ese v¨¦rtice en com¨²n, como se ve en la figura, y de este modo obtenemos los 5 primeros n¨²meros pentagonales, cada uno de los cuales es la suma de su propio per¨ªmetro m¨¢s los anteriores. Como en el caso de los triangulares, se considera que el primer n¨²mero pentagonal es el 1 (el v¨¦rtice com¨²n como pent¨¢gono de lado 0), as¨ª que la secuencia ser¨¢:

1, 5, 12, 22, 35¡­

?Cu¨¢l es el sexto n¨²mero pentagonal?, ?y el s¨¦ptimo?, ?y el d¨¦cimo? ?Hay una f¨®rmula general que nos permita hallar el en¨¦simo n¨²mero pentagonal?

Y, viceversa, dado un n¨²mero cualquiera, ?podemos averiguar f¨¢cilmente si es pentagonal o no?

Los n¨²meros hexagonales se construyen igual que los pentagonales, pero formando, en vez de pent¨¢gonos, hex¨¢gonos sucesivos con un v¨¦rtice com¨²n.

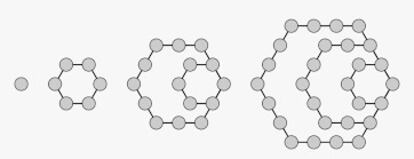
Como se puede ver en la figura, la secuencia es:

1, 6, 15, 28¡­

?Cu¨¢l es el quinto n¨²mero hexagonal?, ?y el sexto?, ?y el d¨¦cimo? ?Hay una f¨®rmula para hallar el en¨¦simo n¨²mero hexagonal?

Y, viceversa, dado un n¨²mero cualquiera, ?c¨®mo podemos averiguar si es hexagonal o no?

El siguiente n¨²mero poligonal es, obviamente, el heptagonal. La secuencia es:

1, 7, 18, 34, 55, 81, 112, 148, 189, 235¡­

Y la f¨®rmula para hallar el en¨¦simo n¨²mero heptagonal es: (5n? ¨C 3n)/2

A¨²n m¨¢s sencilla es la f¨®rmula de los n¨²meros octogonales: 3n? ¨C 2n, cuya secuencia es, por tanto:

1, 8, 21, 40, 65, 96, 133, 176, 225, 280¡­

La f¨®rmula de los n¨²meros decagonales es 4n? ¨C 3n, la misma que la de los octogonales con ambos coeficientes aumentados en una unidad. Y la de los n¨²meros dodecagonales, 5n? ¨C 4n. ?Qu¨¦ nos dice esta secuencia de f¨®rmulas?

Vecinos colaborativos

Los pent¨¢gonos y los hex¨¢gonos, adem¨¢s de ser pol¨ªgonos sucesivos y dar lugar, por ende, a n¨²meros poligonales sucesivos, pueden asociarse para recubrir (convenientemente curvados) superficies esf¨¦ricas, como salta a la vista en el conocido caso del bal¨®n de f¨²tbol. El hex¨¢gono regular es, junto con el tri¨¢ngulo equil¨¢tero y el cuadrado, uno de los tres pol¨ªgonos regulares que pueden ¡°embaldosar¡± el plano. El pent¨¢gono no puede, pero en asociaci¨®n con su vecino da pie a otros interesantes recubrimientos.

?Cu¨¢ntos pent¨¢gonos y hex¨¢gonos hacen falta para recubrir la superficie de una esfera? O lo que es lo mismo, ?de cu¨¢ntas piezas se compone la envoltura de un bal¨®n de f¨²tbol? ?Es ¨²nica la soluci¨®n?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter