Universo distorsionado: de Euclides a Einstein pasando por Plat¨®n

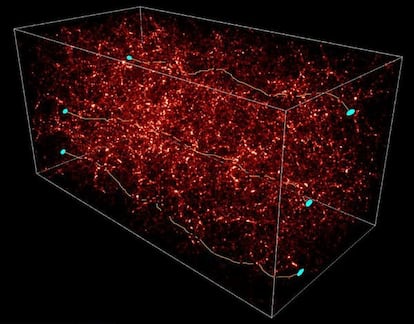
?C¨®mo detectar lo que no puedes ver, lo que no emite luz de ning¨²n tipo, ni de la que ven nuestros ojos, ni infrarroja, ni rayos-X,...? ?C¨®mo detectar la materia oscura pata negra, la ex¨®tica, la que nos gusta a los astrof¨ªsicos pero nadie encuentra en un laboratorio?

Una respuesta nos la dio un tal Albert Einstein hace m¨¢s de un siglo, con la llamada Teor¨ªa General de la Relatividad. M¨¢s de 100 a?os despu¨¦s, esta teor¨ªa va a ser la base de una misi¨®n espacial de la Agencia Espacial Europea, la conocida como Euclid. Con este telescopio, y aplicando lo que nos ense?¨® Einstein, en los pr¨®ximos a?os queremos hacer un mapa de gran precisi¨®n de toda la materia y energ¨ªa del universo.

La misi¨®n Euclid debe su nombre a uno de los griegos que m¨¢s influencia tiene a¨²n hoy en nuestra educaci¨®n y en nuestra mente. Si queremos ir de casa al bar de enfrente, ?ay esos bares!, ?c¨®mo pensamos hacerlo?: en l¨ªnea recta, que es la distancia m¨¢s corta y la forma m¨¢s r¨¢pida de llegar a encontrarnos con los amigos y tomarnos algo cuanto antes. Dos l¨ªneas paralelas nunca se cruzan, eso tambi¨¦n nos lo ense?an desde peque?os. Pues bien, esas dos y otras tres afirmaciones son la base de lo que se conoc¨ªa como geometr¨ªa a secas durante casi dos milenios, pero hoy llamamos geometr¨ªa euclidiana. El matem¨¢tico griego Euclides escribi¨® en su obra ¡°Los elementos¡± gran parte de las nociones de geometr¨ªa que tenemos hoy todos en mente, partiendo solo de esas 5 axiomas o afirmaciones preasumidas (por tanto, no probadas) y demostrando, a partir de ellas, por ejemplo, que la suma de los ¨¢ngulos de un tri¨¢ngulo da 180 grados o el famoso Teorema de Pit¨¢goras. ?Les suena? Verdades irrefutables, ?verdad?

Hoy sabemos que la geometr¨ªa del espacio-tiempo a peque?a escala no es plana, el espacio-tiempo se curva

Llegado el siglo XIX, la geometr¨ªa sufri¨® tal revoluci¨®n que hubo que ponerle un apellido a lo que hasta entonces se hab¨ªa considerado como verdad irrefutable, que pas¨® a llamarse geometr¨ªa euclidiana o plana, porque gran parte de lo que describi¨® Euclides se refiere a formas geom¨¦tricas en un plano, como los tri¨¢ngulos o las l¨ªneas paralelas. Aprendemos sobre ello en el colegio.

Hoy sabemos que la geometr¨ªa del espacio-tiempo a peque?a escala no es plana, el espacio-tiempo se curva. Como consecuencia, los rayos de luz no siguen l¨ªneas rectas sino lo que se conoce como geod¨¦sicas. Y tambi¨¦n como consecuencia, los ¨¢ngulos de un tri¨¢ngulo no tienen por qu¨¦ sumar 180 grados. Es f¨¢cil de comprobar. Podemos formar un tri¨¢ngulo imaginario ¡°caminando¡± por la superficie terrestre. Empezamos andando por el ecuador desde, digamos, las cercan¨ªas de Macap¨¢, en Brasil, hasta encontrarnos con la costa africana m¨¢s o menos en Libreville, Gab¨®n. Giramos entonces 90 grados hacia la izquierda y caminamos recto, lo que supone que nos estamos moviendo por un meridiano hacia el Norte. Llegamos a Europa, pasaremos cerca de Mil¨¢n, Italia, y siguiendo con nuestro paseo imaginario llegaremos al Polo Norte. Ah¨ª giramos unos 96 grados a la izquierda (hacia las 8, dir¨ªan en las pel¨ªculas) y caminamos en l¨ªnea recta de nuevo, siguiendo otro meridiano que nos llevar¨¢ de vuelta a Am¨¦rica del Sur, pasando cerca de Medell¨ªn, Colombia. Cuando nos encontremos con el ecuador, giramos a la izquierda de nuevo 90 grados y llegamos al mismo sitio de nuestro comienzo de viaje. Hemos formado un tri¨¢ngulo sobre la superficie terrestre. Y los ¨¢ngulos suman 273 grados, nada de 180 grados. La superficie de la Tierra no es plana, es un ejemplo de que hay m¨¢s geometr¨ªas posibles que la euclidiana y lo mismo podr¨ªa pasar con el universo, pero en 3 dimensiones espaciales y una temporal.

Volvemos a la misi¨®n Euclid. Y apelamos a otro fil¨®sofo: Plat¨®n. Es famosa la alegor¨ªa en la que unos prisioneros encerrados desde nacimiento en una caverna solo tienen informaci¨®n del exterior a trav¨¦s de las sombras que se proyectan en la pared, deformadas y con una apariencia en gran parte debida a una hoguera que proyecta su luz sobre los objetos reales. Nosotros tambi¨¦n somos prisioneros desde nacimiento, no sabemos c¨®mo es en detalle el universo, e intentamos conocerlo por medio de la luz que nos llega de las galaxias. Los rayos de luz provenientes de galaxias distantes tienen que atravesar un espacio-tiempo curvado por la materia que se encuentra en el camino. El resultado cuando recolectamos los fotones de esas galaxias distantes con nuestros telescopios es que vemos las galaxias deformadas, no como son en realidad. Podr¨ªamos comparar este fen¨®meno con una fuente llena de agua, con monedas desperdigadas por su fondo, como si fuera la Fontana de Trevi (?m¨¢s recuerdos de esos viajes!; ?y de cuando se pod¨ªan tirar monedas a la Fontana!). Si el agua se mueve, por muy transparente que sea, veremos las monedas deformadas.

El Euclid pretende hacer un mapa de toda la materia y energ¨ªa que compone el universo, tanto la visible como la que no emite ni interacciona con los fotones

Aqu¨ª es donde entra en juego el poder de la f¨ªsica y la matem¨¢tica de la Teor¨ªa de Einstein. Estudiando las deformaciones de las galaxias podemos conocer el contenido de materia (y energ¨ªa) del universo, que es el responsable de la curvatura del espacio-tiempo y la consecuente deformaci¨®n de la imagen de las galaxias. La cosa ser¨ªa m¨¢s f¨¢cil conceptualmente si supi¨¦ramos c¨®mo son las galaxias en realidad, si alguien pudiera salir de la cueva de los prisioneros y ver la realidad tal y como es. Eso no es posible, estrictamente hablando. Adem¨¢s, las distorsiones que se forman en la imagen de las galaxias son extremadamente peque?as, las monedas pr¨¢cticamente se ven igual en la analog¨ªa de la fuente. Y, por si fuera poco, las galaxias han ido evolucionando en forma (?c¨®mo las monedas!). Estudiando el mayor n¨²mero de galaxias posibles, en todas las direcciones que podamos, a distintas distancias, lo que pretende Euclid es hacer un mapa de toda la materia y energ¨ªa que compone el universo, tanto la visible como la oscura pata negra, la que no emite ni interacciona con los fotones, no podemos ver, ?ni hemos detectado directamente nunca pero es la m¨¢s abundante del universo!, pero curva el espacio-tiempo.

Euclid se lanzar¨¢ el a?o que viene, si todo va bien, y estar¨¢ tomando datos durante m¨¢s de un lustro. Cuando acabe su misi¨®n tendremos un mejor conocimiento de los componentes del cosmos y cu¨¢n euclidiano o curvo es el universo a peque?a y gran escala. Euclid ser¨¢ como el prisionero que sale de la cueva y luego vuelve a contar a los dem¨¢s c¨®mo es verdaderamente la realidad. Espero que no reneguemos de sus descubrimientos y le matemos, aunque el negacionismo (y el efecto Dunning-Kruger) est¨¢ de moda.

Pablo G. P¨¦rez Gonz¨¢lez es investigador del Centro de Astrobiolog¨ªa, dependiente del Consejo Superior de Investigaciones Cient¨ªficas y del Instituto Nacional de T¨¦cnica Aeroespacial (CAB/CSIC-INTA)

Vac¨ªo C¨®smico es una secci¨®n en la que se presenta nuestro conocimiento sobre el universo de una forma cualitativa y cuantitativa. Se pretende explicar la importancia de entender el cosmos no solo desde el punto de vista cient¨ªfico sino tambi¨¦n filos¨®fico, social y econ¨®mico. El nombre ¡°vac¨ªo c¨®smico¡± hace referencia al hecho de que el universo es y est¨¢, en su mayor parte, vac¨ªo, con menos de 1 ¨¢tomo por metro c¨²bico, a pesar de que en nuestro entorno, parad¨®jicamente, hay quintillones de ¨¢tomos por metro c¨²bico, lo que invita a una reflexi¨®n sobre nuestra existencia y la presencia de vida en el universo. La secci¨®n la integran Pablo G. P¨¦rez Gonz¨¢lez, investigador del Centro de Astrobiolog¨ªa; Patricia S¨¢nchez Bl¨¢zquez, profesora titular en la Universidad Complutense de Madrid (UCM); y Eva Villaver, investigadora del Centro de Astrobiolog¨ªa

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.