Las matem¨¢ticas de los juegos malabares
Los malabaristas utilizan una notaci¨®n num¨¦rica para dise?ar y comunicar sus trucos

No es f¨¢cil ser malabarista. Cada truco requiere pr¨¢ctica y habilidad ¡ªm¨¢s de lo primero que de lo segundo ¡ª y, si se produce un error, este resulta tan evidente como una pelota cayendo al suelo. Tradicionalmente, los malabaristas han aprendido sus trucos los unos de los otros, lo que a?ade una dificultad adicional: ?C¨®mo se explica un truco de malabares?
Explicar un truco con palabras no parece pr¨¢ctico. En su lugar, los malabaristas usan algo parecido a una partitura. En vez de las cinco l¨ªneas horizontales habituales de las partituras musicales, los malabaristas utilizan solo dos, normalmente verticales (En la siguiente imagen est¨¢n representadas horizontalmente). Una representa la mano izquierda y la otra la derecha. A lo largo de estas dos l¨ªneas cada mano realiza una acci¨®n de forma alterna, como si jugasen por turnos. La acci¨®n que realiza normalmente la mano de un malabarista es la de lanzar una pelota u otro objeto. Se representan los lanzamientos dibujando l¨ªneas que van danzando entre ambas manos; a cada pelota se le suele asignar un color.
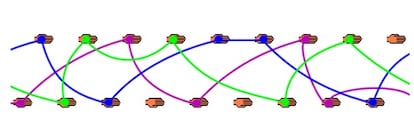
Esta representaci¨®n sigue siendo algo farragosa, ?ser¨¢ posible expresar este truco de un modo m¨¢s pr¨¢ctico y compacto? A principios de los a?os ochenta unos estudiantes del CalTech y la Universidad de Cambridge hallaron la respuesta. Dise?aron la manera de asignar a cada truco de malabares una matr¨ªcula num¨¦rica ¨²nica, la conocida como notaci¨®n Siteswap. La del truco mostrado en la figura es la siguiente: 5314530. Pero, ?por qu¨¦?
La clave de la notaci¨®n Siteswap es contar el n¨²mero de ¡°pasos¡± que tarda un objeto en volver a aterrizar en una mano, la que sea. Lo mejor es verlo con un ejemplo, que se muestra en la siguiente imagen.
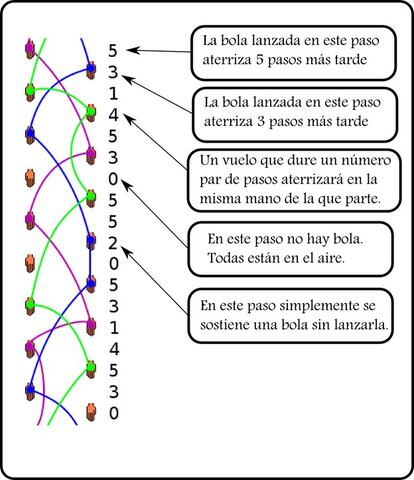
Como se muestra en el ejemplo, hay un par de casos especiales: un 0 representa una mano vac¨ªa, y un 2 representa una mano que sostiene una bola sin lanzarla. Adem¨¢s, la mayor¨ªa de los trucos de malabares repiten un patr¨®n, de modo que la secuencia de n¨²meros se repetir¨¢ una y otra vez.
Entonces, si la secuencia de n¨²meros 5314530 describe de forma ¨²nica e incontrovertible un truco de malabares, todas y cada una de las caracter¨ªsticas y propiedades de dicho truco deben estar contenidas en la secuencia. Sin excepci¨®n.
El n¨²mero tiene que ver con el tiempo que pasa volando la bola, y por tanto con la altura a la que se lanza y hay determinadas propiedades que se observan de forma sencilla en la secuencia de n¨²meros. Por ejemplo, cuando aparece un n¨²mero par, la bola se recoger¨¢ con la misma mano con la que es lanzada; si el n¨²mero es impar, la bola cambiar¨¢ de mano.
Otra propiedad menos obvia es la siguiente: al tomar la media aritm¨¦tica de la secuencia se obtiene el n¨²mero de objetos que se necesita para hacer el truco. En el ejemplo anterior, la media aritm¨¦tica de los elementos de la secuencia 5314530 es (5+3+1+4+5+3+0)/7 = 3. S¨®lo con leer el nombre del truco sabemos cu¨¢ntas pelotas nos har¨¢n falta, sin necesidad de dibujar nada.
Pero a¨²n hay m¨¢s. Tambi¨¦n podemos detectar trucos falsos. Si un malabarista afirma hacer el truco 41, al calcular la media aritm¨¦tica se obtiene (4+1)/2=2,5. ?Un truco con dos pelotas y media? No parece posible y en efecto no lo es (concretamente, porque har¨ªa que dos o m¨¢s pelotas chocasen al mismo tiempo en la misma mano). ?Y no ha habido que hacerlo para descubrirlo!
La notaci¨®n Siteswap es lo suficientemente potente como para usarse en programas inform¨¢ticos de dise?o de trucos y se puede extender a trucos m¨¢s complicados (con objetos que rotan, con varias personas, etc.). Es, adem¨¢s, un excelente ejemplo de c¨®mo las matem¨¢ticas encuentran su aplicaci¨®n en los lugares m¨¢s insospechados.
Pablo Rodr¨ªguez S¨¢nchez (@DonMostrenco) es f¨ªsico, divulgador cient¨ªfico y doctor en matem¨¢ticas aplicadas.
Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.
Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
M¨¢s informaci¨®n

Cinco a?os sin Maryam Mirzakhani, exploradora de superficies





























































