?Por qu¨¦ los peces nadan tan r¨¢pido?

Mientras que el humano m¨¢s r¨¢pido del mundo alcanza una velocidad de unos 10 km por hora en el agua y el submarino m¨¢s veloz, de unos 80 km/h, el pez espada supera f¨¢cilmente 100 km/h al cazar. ?C¨®mo hacen los peces para nadar tan r¨¢pido? Esta inocente pregunta ha tenido en jaque a la comunidad cient¨ªfica durante 50 a?os. En el a?o 2018, el equipo de Tingyu Ming, del Centro de Investigaci¨®n de Ciencias Computacionales de Pek¨ªn (China), resolvi¨® el problema, modelizando de la forma m¨¢s fiel posible el movimiento de los peces.

Hasta entonces, la comunidad estaba dividida entre dos teor¨ªas. La primera, propuesta en 1952 por el f¨ªsico Geoffrey Taylor y la segunda, por el matem¨¢tico James Lighthill en 1960. La diferencia clave entre ambas es el tipo de fuerza generada por el animal que, para sus autores, explica el mecanismo de nataci¨®n. Para Taylor, es una fuerza resistiva, que act¨²a en direcci¨®n opuesta al movimiento del cuerpo, pero est¨¢ directamente relacionada con la velocidad. Para Lighthill, es una fuerza reactiva, que act¨²a en direcci¨®n opuesta a una fuerza de acci¨®n y est¨¢ vinculada a la aceleraci¨®n. Puede parecer una diferencia sutil, pero es clave para comprender la propulsi¨®n de los peces y reproducirla artificialmente.

La teor¨ªa de Taylor ¨Co teor¨ªa de la fuerza resistiva¨C consideraba que el impulso proviene de la interacci¨®n de la superficie del pez con el agua. El agua es un fluido viscoso y, por tanto, genera resistencia al movimiento. Su idea era que la piel del pez, que dividi¨® en peque?os segmentos, genera resistencia, pero, a medida que cada segmento ondula, la resistencia es mayor en la direcci¨®n perpendicular al cuerpo que en la direcci¨®n paralela a ¨¦l. El resultado ¨Cque puede apreciarse en la imagen¨C es un empuje en direcci¨®n paralela, o hacia delante.

La teor¨ªa de Lighthill es algo m¨¢s complicada. Imaginemos una pelota que se mueve sumergida en el agua. La viscosidad del agua, en este caso, se manifiesta en forma de peque?os bloques de fluido que se ven arrastrados, formando torbellinos que viajan en sentido opuesto al que se desplaza la pelota, como puede verse en la Figura 2. En consecuencia, se forma un patr¨®n conocido como calle de v¨®rtices o torbellinos de Von K¨¢rm¨¢n. En condiciones reales aparecen muchos torbellinos, de diferentes tama?os, pero, en promedio, la situaci¨®n es muy similar, como puede verse en la Figura 3.

En este patr¨®n los torbellinos giran en la estela de la pelota, de manera que generan una fuerza, o momento, en el sentido que ¨¦sta se desplaza. Existe una ley de conservaci¨®n que indica que en un sistema cerrado (donde no hay fuerzas externas) la suma de los momentos lineales es siempre constante. Por tanto, para que se conserve la cantidad de momento lineal total, esta fuerza se extrae del desplazamiento de la propia pelota, lo que hace que vaya perdiendo velocidad.

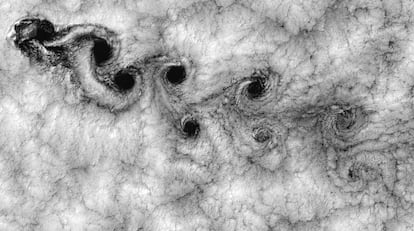
Por este motivo, los submarinos necesitan potentes motores nucleares para poder avanzar a altas velocidades a lo largo de grandes distancias, venciendo la viscosidad del agua. Sin embargo, los peces son capaces de aprovechar este mismo principio a su favor. Con su cola, intercambian la posici¨®n de los v¨®rtices y, as¨ª, se genera una fuerza resultante en el sentido contrario al que viaja el pez. El resultado es una fuerza que empuja al pez, como si se tratara de un motor formado por la acci¨®n combinada de peque?os v¨®rtices, como puede verse en la Figura 4. Este tipo de fuerza se conoce como fuerza reactiva.

Para averiguar cu¨¢l de las dos teor¨ªas era la m¨¢s adecuada, Tingyu Ming y sus colaboradores crearon un modelo hidrodin¨¢mico computacional en tres dimensiones de dos tipos de peces: nadadores anguillifores, como las anguilas, y nadadores carangiformes, como la caballa o el at¨²n. Los primeros ondulan todo su cuerpo, mientras que los segundos solo doblan la mitad trasera. El equipo utiliz¨® datos reales del movimiento de los peces para calibrar sus modelos y as¨ª calcular la fuerza generada por estos tipos de pez.

Esta modelizaci¨®n tan precisa mostr¨® que ambas teor¨ªas son correctas: seg¨²n el tipo de pez e incluso la parte del cuerpo del animal que estemos considerando, la descripci¨®n viene dada por una u otra. Por ejemplo, tanto para la caballa y para la anguila, las fuerzas resistivas son m¨¢s importantes en la parte media del cuerpo, pero las fuerzas reactivas son m¨¢s importantes cerca de las colas.

El trabajo mostr¨® que la propulsi¨®n de los peces es mucho m¨¢s compleja de lo que se pensaba y, presumiblemente, igual de dif¨ªcil de reproducir de forma artificial. Aunque la investigaci¨®n al respecto es muy incipiente, estos avances suponen una base te¨®rica para futuros desarrollos de submarinos m¨¢s r¨¢pidos, de veh¨ªculos subacu¨¢ticos m¨¢s eficientes que permitan explorar el oc¨¦ano de manera menos invasiva o hasta de m¨¦todos para viajar que generen menos contaminaci¨®n ac¨²stica ¨Cque es una de las causas de p¨¦rdida de biodiversidad en los mares de todo el mundo¨C.

Guillermo Garc¨ªa S¨¢nchez es investigador predoctoral en el ICMAT.

?gata Tim¨®n G. Longoria es coordinadora de la Unidad de Cultura Matem¨¢tica del ICMAT.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.