Una f¨®rmula para tiburones: las ecuaciones que comparten ec¨®logos y economistas

En todos los ecosistemas los seres vivos se relacionan de formas similares. Ya se trate de un desierto o una charca, siempre podemos encontrar especies que mantienen v¨ªnculos de competencia, simbiosis, parasitismo, depredaci¨®n¡­ Estas interacciones se pueden simular con sistemas de ecuaciones diferenciales, cuyas soluciones describen el comportamiento esperado a lo largo del tiempo. Un ejemplo de estos modelos biol¨®gicos es el propuesto por el biof¨ªsico Alfred J. Lotka y el matem¨¢tico Vito Volterra ¡ªde manera independiente¡ª en la d¨¦cada de 1920, que es capaz de describir las relaciones entre depredadores y presas.

El llamado modelo de Lotka-Volterra se us¨® por primera vez para responder a una cuesti¨®n planteada por el bi¨®logo marino Umberto d¡¯Ancona. Este hab¨ªa observado que, durante la Primera Guerra Mundial, los pescadores del mar Adri¨¢tico capturaban un porcentaje mayor de lo habitual de tiburones, rayas y otros grandes depredadores. D¡¯Ancona achac¨® esta anomal¨ªa a la disminuci¨®n de la actividad pesquera causada por la guerra. Sin embargo, resultaba extra?o que esta reducci¨®n no beneficiase m¨¢s a las especies medianas, m¨¢s consumidas por el ser humano. Intrigado, consult¨® el problema con Volterra. El matem¨¢tico quiso describir, mediante un par de ecuaciones, c¨®mo este cambio afectaba al n¨²mero promedio de presas y depredadores.

Para ello, ide¨® un sistema de dos ecuaciones que refleja la interconexi¨®n entre las dos especies, cuyas inc¨®gnitas son el n¨²mero de presas ¡ªpor ejemplo, peces de tama?o mediano¡ª, representado por la variable x, y de depredadores ¡ªtiburones¡ª, representado por y. Las ecuaciones incluyen cuatro par¨¢metros fijos: A, que representa la tasa de reproducci¨®n de las presas; B, que se relaciona con la probabilidad de que una presa sea cazada; C, la tasa de mortalidad de los predadores; y D, relacionada con la proporci¨®n de capturas necesarias para la reproducci¨®n de los depredadores. Las ecuaciones establecen los valores de las derivadas x¡¯ e y¡¯, que representan la variaci¨®n de las poblaciones en el tiempo, respecto a las variables y par¨¢metros anteriores.

La primera ecuaci¨®n indica que la variaci¨®n del n¨²mero de presas, partiendo de una poblaci¨®n de presas de x individuos y de depredadores de y, es igual a Ax, la cantidad de presas que nacen, menos Bxy, que representa el n¨²mero de presas capturadas en la caza. Por otro lado, la segunda ecuaci¨®n establece que la variaci¨®n de los depredadores es Dxy, los depredadores que nacen gracias al alimento conseguido, menos Cy, los depredadores fallecidos.

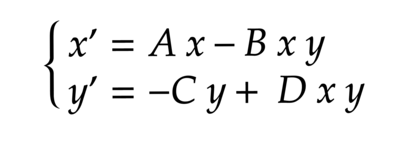
En este modelo, cuando no existen depredadores, las presas se reproducen a un ritmo exponencial, sin l¨ªmite. Por otro lado, la ausencia de presas lleva a que los depredadores se extingan y, cuantos m¨¢s individuos tengan que competir por el escaso alimento disponible, m¨¢s r¨¢pido decrecer¨¢ la poblaci¨®n.

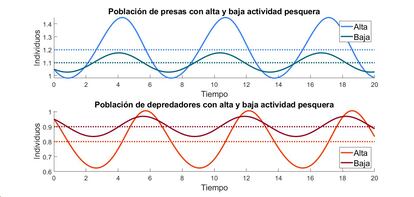
En cualquier otro caso, las ecuaciones establecen que, a lo largo del tiempo, ambas poblaciones fluct¨²an peri¨®dicamente en torno a unos valores promedio, dados por C/D para las presas y por A/B para los depredadores ¡ªen la imagen, se?alados con l¨ªneas discontinuas¡ª. Si se introduce la actividad pesquera en las ecuaciones con un nuevo par¨¢metro E, se obtiene un efecto equivalente a reducir la tasa de natalidad de las presas ¡ªcambiando A por A-E¡ª y a aumentar la tasa de mortalidad de los depredadores ¡ªpasando de C a C+E¡ª. De esta forma, un descenso de la actividad pesquera, es decir, de E, se traduce en un crecimiento del n¨²mero medio de depredadores ¡ª(A-E)/B¡ª y una reducci¨®n del de las presas ¡ª(C+E)/D¡ª, que es justo lo que observ¨® d¡¯Ancona.

La utilidad del modelo presa-depredador no se limita a la ecolog¨ªa. En 1967, el economista Richard M. Goodwin emple¨® estas ecuaciones para explicar las fluctuaciones econ¨®micas como una consecuencia de los desajustes entre mano de obra y salarios. Concretamente, plante¨® que la tasa de empleo y el coste de los salarios son variables que evolucionan c¨ªclicamente, de forma similar al n¨²mero de presas y depredadores. La propuesta de Goodwin para describir el mercado laboral introdujo una nueva idea en econom¨ªa te¨®rica: su modelo matem¨¢tico daba una interpretaci¨®n de los ciclos propios del capitalismo a trav¨¦s de causas end¨®genas al sistema, sin necesidad de recurrir a shocks externos.

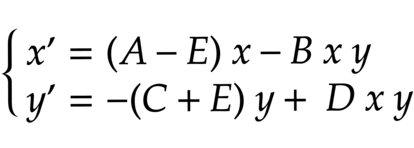
Pese a su simplicidad, las ecuaciones de Lotka-Volterra sirven para modelizar diversos sistemas complejos y, hoy en d¨ªa, siguen aplic¨¢ndose en numerosos casos. Adem¨¢s, en los ¨²ltimos a?os se han introducido diversas variaciones con el fin de simular situaciones m¨¢s complejas, como por ejemplo interacciones entre un mayor n¨²mero de especies, fen¨®menos de canibalismo entre los depredadores o estrategias defensivas de las presas. El sistema de Lotka-Volterra fue uno de los primeros en la historia de la modelizaci¨®n matem¨¢tica, un camino de ¨¦xito que han seguido muchos de los modelos utilizados hoy en d¨ªa en ramas aparentemente tan alejadas como la meteorolog¨ªa o la epidemiolog¨ªa.

Alba Garc¨ªa Ruiz y Enrique Garc¨ªa S¨¢nchez son investigadores predoctorales del Consejo Superior de Investigaciones Cient¨ªficas en el Instituto de Ciencias Matem¨¢ticas.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.