El tablero astron¨®mico

EL PA?S y Materia proponen a sus lectores, cada semana, un juego de l¨®gica. Los lectores pueden enviar sus soluciones en los comentarios, y plantear nuevos acertijos y juegos. La respuesta correcta ser¨¢ ofrecida en la columna de la semana siguiente.

La recompensa que el m¨ªtico inventor del ajedrez le pidi¨® al rey de la India constituye uno de los m¨¢s conocidos ejemplos del vertiginoso crecimiento de las progresiones geom¨¦tricas. Un grano de trigo por la primera casilla del tablero, dos por la segunda, cuatro por la tercera, ocho por la cuarta¡­ La intuici¨®n nos dice que con un saco de trigo ser¨¢ suficiente, y sin embargo no bastar¨ªa la cosecha mundial de muchos a?os para suministrar los aproximadamente 18 trillones y medio de granos resultantes.

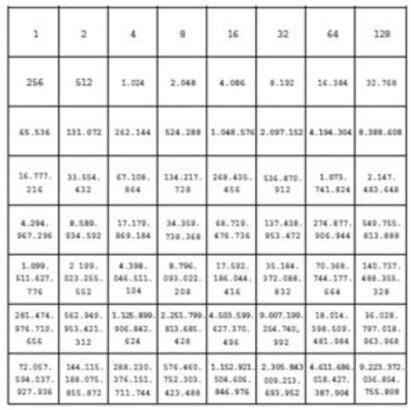
El c¨¢lculo es sencillo, sin necesidad de echar mano de las f¨®rmulas matem¨¢ticas: basta con ver que los granos de cada casilla superan en una unidad a los de todas las anteriores juntas: 2=1+1, 4=2+1+1, 8=4+2+1+1¡­ En la casilla 64?, tras 63 duplicaciones, habr¨¢ 2⁶³ granos, luego en todas las anteriores juntas habr¨¢ 2⁶³-1, y en total: 2⁶³+2⁶³-1=2⁶⁴-1.

En cuanto a la torre de Han¨®i, hemos visto que para trasladar tres discos (numerados de menor a mayor: 1, 2 y 3) son necesarios un m¨ªnimo de siete movimientos, siguiendo la secuencia 1213121. Ahora bien, para dos discos la secuencia es 121, o sea, que lo que hemos hecho ha sido trasladar una torre de dos discos, luego desplazar el tercer disco y por ¨²ltimo volver a trasladar la torre de dos discos para ponerla encima del tercero. Es f¨¢cil comprobar que, an¨¢logamente, con cuatro discos la secuencia es 121312141213121: primero trasladamos una torre de tres discos, luego desplazamos el cuarto, y por ¨²ltimo volvemos a trasladar la torre de tres para ponerla encima del cuarto disco. Y as¨ª sucesiva e indefinidamente.

As¨ª pues, a medida que aumenta el n¨²mero de discos, el n¨²mero de movimientos necesarios para trasladarlos crece seg¨²n la progresi¨®n 1, 1+1+1=3, 3+1+3=7, 7+1+7=15, 15+1+15=31¡­ Pero 1, 3, 7, 15, 31¡­ son las sucesivas potencias de 2 menos 1; por lo tanto, para trasladar una torre de 64 discos har¨¢n falta 2⁶⁴-1 movimientos, tantos como granos de trigo le pidiera al rey de la India el inventor del ajedrez.

Un n¨²mero astron¨®mico, sin duda, pero ni mucho menos el mayor de los que pueden proliferar en un damero. Consideremos, sin ir m¨¢s lejos, el n¨²mero de jugadas posibles en una partida de ajedrez. En su primera jugada, las blancas tienen 20 opciones (adelantar una o dos casillas cada uno de los ocho peones y mover cada caballo a una de las dos casillas accesibles), y a cada apertura pueden responder las negras, asimismo, de 20 maneras distintas, con lo que tenemos 400 combinaciones posibles. Tras el segundo movimiento de las blancas, las situaciones posibles son ya m¨¢s de 5.000, y m¨¢s de 70.000 tras el segundo movimiento de las negras (exactamente 72.084). Tras el tercer movimiento de las blancas hay m¨¢s de 800.000 posiciones posibles, y m¨¢s de 9.000.000 tras el tercero de las negras¡­ Si sigui¨¦ramos adelante, llegar¨ªamos a una cifra del orden de los septillones, frente a la cual los 18 trillones y medio de granos de trigo del inventor del ajedrez se convierten en una insignificante migaja.

Pero volvamos a los n¨²meros abarcables: acabamos de ver que las situaciones posibles tras el segundo movimiento de las blancas son m¨¢s de 5.000, pero¡­ ?cu¨¢ntas son exactamente?

Y hablando de las primeras jugadas del ajedrez, ?cu¨¢l es la partida m¨¢s corta posible?

Carlo Frabetti

Escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York, ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯