El poder de los indecisos

Las citas electorales se han incorporado a nuestro calendario como el d¨ªa de San Valent¨ªn o de la Constituci¨®n. En las semanas previas comienza la avalancha de datos, estimaciones y comentarios en torno al m¨¦todo de reparto de esca?os. El matem¨¢tico y periodista americano George Gallup introdujo los sondeos electorales en los a?os 30. Estos estudios tratan de predecir el resultado electoral y buena parte del electorado los considera autom¨¢ticamente objetivos, sin considerar su margen de error ni valorar las t¨¦cnicas estad¨ªsticas empleadas.

Sin embargo, es importante hacer algunas consideraciones matem¨¢ticas sobre los resultados que se presentan. Hay un rico conjunto de herramientas matem¨¢ticas (el Teorema Central del L¨ªmite, la Ley de los Grandes N¨²meros, las t¨¦cnicas estad¨ªsticas para construir muestras, para acotar el error, etc.) que permite asegurar que los resultados de un estudio muestral son significativos. Ahora bien, suponiendo que todo se realice siguiendo las t¨¦cnicas estad¨ªsticas adecuadas (y esto es mucho suponer), el sondeo muestra unos resultados con un margen de error, un intervalo en el que se podr¨ªa encontrar el valor verdadero con una probabilidad suficientemente alta. Se trata de datos del voto directo, donde las matem¨¢ticas garantizan que las afirmaciones tienen un valor de verdad hasta el porcentaje de error indicado. Sin embargo, no a todo el mundo le resulta sencillo tomar una decisi¨®n. ?C¨®mo se refleja esta incertidumbre en los sondeos? ?Influyen los indecisos en los resultados electorales?

La duda suele crecer a medida que se acercan las elecciones. Algunos soci¨®logos lo establecen entre el 20% y el 50%. Pero las empresas que hacen los sondeos han de realizar una estimaci¨®n de ese voto, como si fuera el d¨ªa de las elecciones y estos ciudadanos hubieran escogido finalmente a uno de los candidatos. Por tanto, se les asigna un voto hipot¨¦tico bas¨¢ndose en la informaci¨®n obtenida a trav¨¦s de preguntas como: ?con qu¨¦ partido simpatiza usted m¨¢s?, ?a qu¨¦ partido se siente usted m¨¢s cercano? o ?a qu¨¦ partido vot¨® usted en las ¨²ltimas elecciones? De esta manera se introduce una estimaci¨®n, y sea cual sea la f¨®rmula que se utilice, no deja de ser un riesgo que asume la empresa demosc¨®pica. Los soci¨®logos son humanos y el clima de opini¨®n puede influir en el modo de asignaci¨®n del voto indeciso. Por tanto, el resultado no es un dato indiscutible, y tomarlo como tal conduce a decisiones err¨®neas.

?C¨®mo se refleja esta incertidumbre en los sondeos? ?Influyen los indecisos en los resultados electorales?

De hecho, como consecuencia de esta forma de manejar los datos, muchos de los informes de los sondeos incluyen un p¨¢rrafo que dice que el reparto de esca?os que se calcula no tiene consistencia estad¨ªstica. Y no tiene por qu¨¦ vaticinar la situaci¨®n real del d¨ªa de las elecciones. En ese momento, mantener la indecisi¨®n se traducir¨ªa en votar en blanco, lo que tambi¨¦n influye en el resultado. No considero que la abstenci¨®n sea una indecisi¨®n, de hecho afecta de diferente manera al reparto de votos. El sistema electoral espa?ol distribuye los esca?os siguiendo el m¨¦todo D¡¯Hont (Rafa H?hr lo explicaba en este art¨ªculo). Para tener representaci¨®n parlamentaria en Espa?a, un partido necesita un m¨ªnimo del 3% de los votos v¨¢lidos en la circunscripci¨®n. Imaginemos que en una circunscripci¨®n electoral 100.000 votantes se decantan por alg¨²n partido y 50.000 se abstienen. Cada partido necesitar¨¢ un m¨ªnimo de 3.000 votos para obtener representaci¨®n parlamentaria. Sin embargo, si 100.000 electores votan a diferentes partidos y 50.000 votan en blanco, cada partido necesitar¨ªa 4.500 votos. Esto supone una importante cantidad de votos m¨¢s, que perjudica a los partidos minoritarios.

La indecisi¨®n tambi¨¦n es clave en la formaci¨®n de gobierno. Hasta la jornada electoral la duda est¨¢ en los ciudadanos, el d¨ªa despu¨¦s comienza la indeterminaci¨®n de los partidos pol¨ªticos para decidir el sentido de su voto. Este juego de psicoprobabilidad ilustra la situaci¨®n:

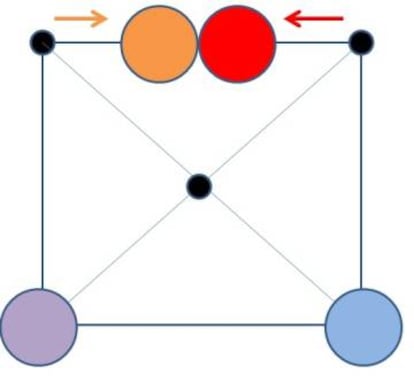
¡°Hay cuatro jugadores (morado, rojo, azul, naranja) y cada uno puede votar a un candidato (tambi¨¦n a s¨ª mismo). Cada uno est¨¢ situado en los v¨¦rtices de un cuadrado y tiene los ojos vendados. Cuando el ¨¢rbitro d¨¦ la se?al, sin hacer ruido, cada jugador puede quedarse quieto o moverse por alguno de los dos lados o la diagonal que sale desde su v¨¦rtice. Cuando dos o m¨¢s jugadores se encuentran, pactan. Ganas si consigues acumular un grupo con el mayor n¨²mero de votos, y pierdes si alguno de los dem¨¢s ha formado un grupo con m¨¢s votos que t¨². Si ning¨²n jugador consigue formar un grupo con mas votos que los dem¨¢s, todos vuelven a la posici¨®n inicial y comienza el juego de nuevo. Esta es la segunda vez que juegas, y en la primera, el rojo y el naranja se encontraron y el azul y el morado se quedaron quietos. En esta ronda, ?qu¨¦ estrategia seguir¨ªan? Podr¨ªan permanecer quietos o moverse hacia uno de los v¨¦rtices pero ?hacia cu¨¢l? y ?por qu¨¦?¡±

Tambi¨¦n estas preguntas se tratan de resolver con las matem¨¢ticas, con la Teor¨ªa de Juegos. All¨ª entra la teor¨ªa del equilibrio de Nash, o quiz¨¢s, con m¨¢s aplicaci¨®n en las circunstancias actuales, la teor¨ªa de juegos cooperativa.

Antonio Moreno Verdejo es profesor del Departamento de Did¨¢ctica de la Matem¨¢tica de la Universidad de Granada