Pi, Indiana y legisladores con poco criterio
?Puede alguna ley influir directamente en hechos demostrados matem¨¢ticamente? Quiz¨¢s no deber¨ªa, pero hubo un momento de la historia en el que estuvo a punto de hacerlo.

Creo que estar¨¦is de acuerdo conmigo en que todo lo que gira alrededor de las leyes es complicado, tanto lo que se refiere a su creaci¨®n como a su aplicaci¨®n. La influencia que tienen sobre nuestra vida es tal que el ¡°noble¡± arte de legislar conlleva una gran responsabilidad para quien tiene que ¡°practicarlo¡±. Pero ello no impide que de vez en cuando nos topemos con alguna ley ¡°peculiar¡±, por decirlo de alguna forma. En el mundo de internet aparecen de forma recurrente listas con algunas leyes que sin lugar a dudas podr¨ªamos calificar como absurdas. Por poner un par de ejemplos, parece ser que en Florida (EEUU) las mujeres solteras que salten en paraca¨ªdas los domingos pueden ser encarceladas; y en Reino Unido se considera acto de traici¨®n poner al rev¨¦s un sello de correos en el que aparezca una imagen de la monarqu¨ªa brit¨¢nica.
Bien, pues va a ser de esto de lo que vamos a hablar, No, de la monarqu¨ªa brit¨¢nica no, de leyes absurdas. En concreto de un proyecto de ley que estuvo a punto de fructificar en Indiana a finales del siglo XIX con el que, b¨¢sicamente, se habr¨ªa conseguido legislar en contra de una verdad matem¨¢tica ya demostrada.
Antes de entrar en la historia en s¨ª, es fundamental dejar algo bien claro: la cuadratura del c¨ªrculo con regla y comp¨¢s es imposible. Quiz¨¢s con la versi¨®n larga de esa afirmaci¨®n la cosa se entienda mejor:
Dado un c¨ªrculo del cual conocemos su radio, es imposible obtener un cuadrado cuya ¨¢rea sea la misma que la del c¨ªrculo inicial utilizando regla y comp¨¢s y las normas de utilizaci¨®n de estas dos herramientas que estaban aceptadas en la antigua Grecia para las construcciones ideales
Sin entrar en detalles, la raz¨®n por la que este problema no se puede resolver es que ¦Ð (s¨ª, el n¨²mero Pi de toda la vida, 3,14159¡) es un n¨²mero de los llamados trascendentes (que son los n¨²meros que no son soluci¨®n de ning¨²n polinomio cuyos coeficientes sean n¨²meros enteros), hecho que fue demostrado en 1882 (repito, en 1882, quedaos con esto) por el matem¨¢tico alem¨¢n Ferdinand von Lindemann.
Nuestra historia (cuya versi¨®n resumida comentaron en Verne hace unos meses) se sit¨²a en Indiana (EEUU) en el a?o 1897, cuando Edwin J. Goodwin, m¨¦dico y matem¨¢tico aficionado, le propuso al representante pol¨ªtico Taylor I. Record un proyecto de ley, el n¨²mero 246 de aquella sesi¨®n, cuyo t¨ªtulo, agarraos a lo que teng¨¢is a mano, acab¨® siendo el siguiente:
Un proyecto de ley que presenta una nueva verdad matem¨¢tica y que es ofrecido como una contribuci¨®n a la educaci¨®n que s¨®lo podr¨¢ ser utilizado por el Estado de Indiana en forma gratuita sin necesidad de pagar ning¨²n tipo de royalties, siempre y cuando sea aceptado y adoptado en forma oficial por la legislatura en 1897
Dicho proyecto no era m¨¢s que una demostraci¨®n incorrecta del problema de la cuadratura del c¨ªrculo (pod¨¦is ver su contenido aqu¨ª). S¨ª, en 1897, quince a?os despu¨¦s de que se demostrara que dicho problema no ten¨ªa soluci¨®n.

El caso es que Record present¨® el proyecto y la Casa de Representantes lo env¨ªo al Comit¨¦ de Canales, que a su vez lo deriv¨® al Comit¨¦ de Educaci¨®n. ?ste ¨²ltimo dio una opini¨®n positiva sobre el mismo (??), por lo que la Casa de Representantes lo aprob¨® por unanimidad: 67 votos a favor y 0 en contra. El siguiente paso era el env¨ªo del proyecto n¨²mero 246 al Senado para su m¨¢s que probable aprobaci¨®n (vistos los antecedentes) y, por tanto, su establecimiento como ley.
Y aqu¨ª es donde aparece el ¡°h¨¦roe¡± de esta historia: Clarence Abiathar Waldo, matem¨¢tico estadounidense. Waldo hab¨ªa acudido a gestionar el presupuesto anual de la Academia de Ciencias de Indiana cuando se enter¨® de que se estaba debatiendo un proyecto de ley relacionado con las matem¨¢ticas y se qued¨® a escuchar. La cara que se le debi¨® quedar debi¨® ser digna de inmortalizar para la posteridad.
Al finalizar el debate, uno de los Representantes le entreg¨® una copia del proyecto y le ofreci¨® presentarle al ¡°genio¡± Goodwin. La respuesta de Waldo lo dice todo:
Ya conozco a tantos locos como puedo soportar
Pero, evidentemente, el bueno de Waldo no pod¨ªa dejar que la historia quedara as¨ª. Esa misma tarde estuvo explicando a los Senadores el contenido del proyecto 246 y haci¨¦ndoles ver la barbaridad que aprobar¨ªan si votaban a favor del mismo. Y tuvo ¨¦xito, ya que consigui¨® convencer a un n¨²mero suficiente de ellos para que no lo hicieran, quedando el proyecto pospuesto indefinidamente.
Por cierto, cuenta la historia que en aquella reuni¨®n en el Senado hubo tanto ridiculizaciones del proyecto como indignaci¨®n por hacer gastar el dinero del ciudadano en tama?a frivolidad (aqu¨ª pod¨¦is encontrar todo lo que ocurri¨® el d¨ªa de marras).
Acabada la historia (con final feliz, por suerte), queda por descubrir qu¨¦ tiene que ver el proyecto 246 con el n¨²mero Pi. De hecho, en el mismo ni se menciona dicho n¨²mero, pero s¨ª podemos encontrar en ¨¦l la siguiente aseveraci¨®n, consecuencia de la err¨®nea resoluci¨®n de Goodwin del problema de la cuadratura del c¨ªrculo:
La raz¨®n entre el di¨¢metro de una circunferencia y su longitud es cinco cuartos a cuatro
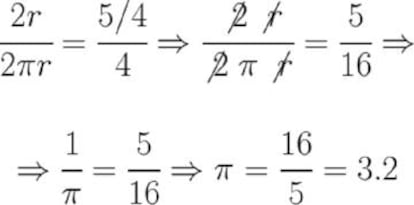
Si recordamos que dada una circunferencia de radio r su di¨¢metro es 2r y la longitud de la misma es 2¦Ðr, esta frase nos da una expresi¨®n matem¨¢tica de la que podemos despejar f¨¢cilmente el valor de Pi:
Es decir, la aprobaci¨®n del proyecto 246 habr¨ªa supuesto establecer por ley que el valor del n¨²mero ¦Ð es 3.2, y con ello, por ejemplo, su utilizaci¨®n en libros de texto de Indiana (gratis, eso s¨ª) y el cobro de ¡°derechos¡± por su uso fuera de dicho estado. Una aberraci¨®n a todas luces.
Esperemos que los legisladores actuales mediten y debatan m¨¢s sobre las leyes de lo que lo hicieron en aquel momento los de Indiana para que no se les ¡°cuelen¡± barbaridades como ¨¦sta.
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.




























































