La circunferencia de Feuerbach o por qu¨¦ me encantan los tri¨¢ngulos

El tema que nos ocupa hoy puede ser considerado como una de esas ¡°sorpresas¡±. Vamos a explicarlo detenidamente, pasa as¨ª poder percibir todos los detalles de esta maravilla de la geometr¨ªa plana.

Tomamos un tri¨¢ngulo plano cualquiera, el que sea, y marcamos en ¨¦l los puntos medios de cada uno de sus lados. Podemos ahora dibujar una circunferencia que pase por esos tres puntos:

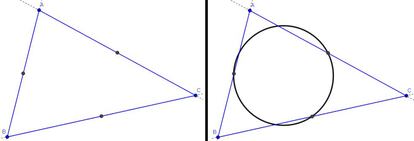
Hasta ahora poca sorpresa, ya que por tres puntos no alineados pasa una ¨²nica circunferencia. Vamos, lo normal.

Dibujamos ahora las tres alturas del tri¨¢ngulo, que son los tres segmentos que van desde cada uno de los v¨¦rtices a la recta a la que pertenece el lado opuesto a dicho v¨¦rtice y que son perpendiculares a esa recta. Si marcamos ahora los tres puntos de intersecci¨®n de estas alturas con las rectas opuestas, se tiene que ¡°curiosamente¡± dichos puntos tambi¨¦n est¨¢n en la circunferencia anterior:

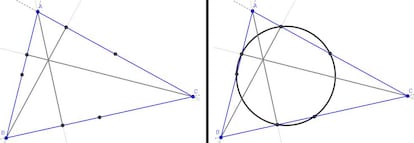
Aqu¨ª la cosa comienza a ser interesante. Como hemos dicho, que tres puntos no alineados est¨¦n en una circunferencia es obligatorio, pero que sean ya seis puntos los que caen en la misma circunferencia tiene su gracia.

Pero a¨²n hay m¨¢s.

Como muchos habr¨¦is advertido, las tres alturas que hemos dibujado se cortan en un punto, que se denomina ortocentro. Bien, localizado el ortocentro marquemos ahora los puntos medios entre este punto y cada uno de los v¨¦rtices. Obtenemos as¨ª tres nuevos puntos¡­??que tambi¨¦n est¨¢n en la circunferencia anterior!!

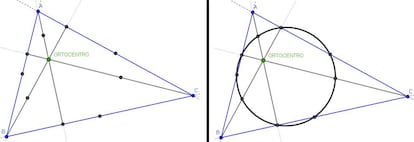
Ya no son tres (lo normal) ni seis (interesante) los puntos calculados que caen en la misma circunferencia, sino nueve. El inter¨¦s se torna ahora en sorpresa y, por qu¨¦ no, en incredulidad. Pues no hay raz¨®n para ser incr¨¦dulo en este caso. Dicha circunferencia se denomina circunferencia de los nueve puntos, y el hecho de que esos nueves puntos caigan en dicha circunferencia es un teorema matem¨¢tico (vamos, que tiene su demostraci¨®n).

Pero no queda ah¨ª la cosa. Tenemos una circunferencia a la que pertenecen nueve puntos que podemos agrupar en tres grupos de tres puntos dependiendo de la manera en la que los hemos encontrado. Pero lo que tenemos es una circunferencia. ?Y cu¨¢l es el punto m¨¢s representativo de una circunferencia? Pues, posiblemente, es el centro. ?Por d¨®nde caer¨¢ el centro de nuestra interesante circunferencia? ?Estar¨¢ por ah¨ª, digamos, situado aleatoriamente? ?O, por el contrario, tendr¨¢ alguna relaci¨®n con el tri¨¢ngulo? Ve¨¢moslo.

Record¨¢is que ten¨ªamos calculado el ortocentro del tri¨¢ngulo, ?verdad? Pues vamos a calcular otro punto relacionado con un tri¨¢ngulo. Trazamos las mediatrices de cada lado del tri¨¢ngulo (son las rectas perpendiculares a cada lado y que pasan por los puntos medios de los mismos), y advertimos que las tres se cortan en un ¨²nico punto. Ese punto se denomina circuncentro.

Bien, pues se da la circunstancia de que el centro de la circunferencia de los nueve puntos es, exactamente, el punto medio del segmento que une el ortocentro con el circuncentro. No solamente en nuestro tri¨¢ngulo, ni en un tri¨¢ngulo con unas caracter¨ªsticas espec¨ªficas, sino en todos los tri¨¢ngulos. ?No os parece hermoso?

Para que pod¨¢is visualizar mejor todo esto, os dejo un applet interactivo de GeoGebra con todo lo que hemos contado. Pod¨¦is mover los v¨¦rtices del tri¨¢ngulo y ver que en todos los casos esos nueve puntos est¨¢n en la misma circunferencia. Tambi¨¦n pod¨¦is comprobar que el punto medio del segmento que une el ortocentro con el circuncentro es el centro de nuestra circunferencia viendo que todos los segmentos que unen dicho punto con los nueve anteriores siempre miden lo mismo:

Y en este pdf ten¨¦is informaci¨®n sobre c¨®mo demostrar este resultado, entre otras muchas cosas relacionadas con geometr¨ªa.

La circunferencia de los nueve puntos tambi¨¦n es conocida como la circunferencia de Feuerbach, porque el matem¨¢tico alem¨¢n Karl Feuerbach (hermano del fil¨®sofo Ludwig Feuerbach) descubri¨® que la circunferencia pasaba por los puntos medios de los lados y tambi¨¦n por los cortes de las alturas (los seis primeros puntos que hemos comentado en la construcci¨®n anterior), pero tambi¨¦n se conoce con el nombre de circunferencia de Euler (aunque parece ser que no hay razones significativas para atribuir a Euler algo relacionado con este resultado). El primero que descubri¨® que la circunferencia tambi¨¦n pasa por los puntos medios de los segmentos que unen el ortocentro con los v¨¦rtices fue el matem¨¢tico franc¨¦s Olry Terquem.

Como hab¨¦is podido comprobar, no hay ninguna duda de que esta circunferencia de Feuerbach es uno de los objetos geom¨¦tricos m¨¢s interesantes que se pueden encontrar en geometr¨ªa plana. Pero seguro que muchos de vosotros conoc¨¦is otros teoremas geom¨¦tricos dignos de ser citados. Estaremos muy agradecidos si nos habl¨¢is de ellos en los comentarios.