Una f¨®rmula para dominarlos a todos (los poliedros convexos)

Echa un vistazo al lugar en el que te encuentres ahora: tu habitaci¨®n, el sal¨®n de tu casa, la oficina o lo que alcances a ver desde el parque o la parada de autob¨²s en la que est¨¦s ahora mismo. Estoy casi seguro de que est¨¦s donde est¨¦s podr¨¢s encontrar algo en forma de caja (aunque no sea perfecta). S¨ª, una caja ¡°de las de toda la vida¡±, como las t¨ªpicas cajas de zapatos. Da igual si se acerca m¨¢s a un cubo, tambi¨¦n nos vale.

Ya tenemos la caja, ?verdad? Pues ahora f¨ªjate en ella y cuenta sus caras (los pol¨ªgonos que la limitan), aristas (l¨ªneas que unen dos caras) y v¨¦rtices (puntos donde se cortan varias aristas). Si la caja es de las habituales, tendr¨¢ 6 caras, 12 aristas y 8 v¨¦rtices, ?a que s¨ª? Bien, pues ahora haz esta operaci¨®n: caras ¨C aristas + v¨¦rtices. ?Resultado? F¨¢cil: 2.

Busca ahora una figura tridimensional de este estilo pero m¨¢s compleja, con m¨¢s elementos que una t¨ªpica caja, pero que no tenga ¡°entrantes¡± (pronto concretaremos m¨¢s este punto). Si no encuentras ninguna cerca, puedes imaginar que a tu caja le quitas un pico cortando con una sierra. Visualiza mentalmente la figura que queda y cuenta de nuevo caras, aristas y v¨¦rtices.

En este caso tendr¨ªas 7 caras (porque al cortar como hemos dicho has creado una cara m¨¢s), 15 aristas (las anteriores y las tres del tri¨¢ngulo que has creado al cortar) y 10 v¨¦rtices (creas tres nuevos pero eliminas uno). Ahora haz de nuevo la operaci¨®n anterior: caras ¨C aristas + v¨¦rtices. ?Cu¨¢l es el resultado? Exacto: de nuevo 2.

Si no conoces el tema del que vamos a hablar hoy, podr¨ªas pensar que esto es casualidad. Probemos con otra m¨¢s, por ejemplo una pir¨¢mide como las de Egipto. Estas pir¨¢mides tienen 5 caras (las cuatro laterales y la base), 8 aristas (las cuatro de las caras laterales y las cuatro de la base) y 5 v¨¦rtices (el superior y los cuatro de la base). Realizamos de nuevo la operaci¨®n anterior, caras ¨C aristas + v¨¦rtices y¡­otra vez obtenemos 2 como resultado. Puedes probar con otras figuras, como los s¨®lidos plat¨®nicos (uno de ellos, el cubo, es esencialmente el mismo ejemplo que la caja):

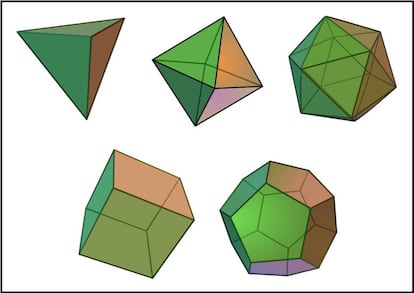
Como muchos lectores habr¨¦is adivinado, el tema de hoy es la conocida como f¨®rmula de Euler para poliedros, una de esas maravillas que muy de vez en cuando nos encontramos en matem¨¢ticas. El resultado relacionado con ella podr¨ªa enunciarse as¨ª:

En un poliedro convexo con C caras, A aristas y V v¨¦rtices, siempre se cumple que C ¨C A + V=2.

Un poliedro es una figura tridimensional limitada por pol¨ªgonos que encierra un volumen concreto (finito), como la caja o la pir¨¢mide que hemos usado antes. Y es convexo cuando no tiene entrantes ni agujeros. Por aclarar esto un poco m¨¢s, un poliedro es convexo si al unir con un segmento dos puntos cualesquiera del poliedro, dicho segmento queda completamente en el interior del poliedro.

Volvamos a la f¨®rmula. Es conocida como f¨®rmula de Euler porque fue el grand¨ªsimo matem¨¢tico suizo Leonhard Euler quien habl¨® sobre ella por primera vez en su trabajo Elementa doctrinae solidorum, escrito en 1750 y publicado en 1758. Euler la escrib¨ªa de la forma C + V = A + 2, y se puede deducir que sab¨ªa que s¨®lo era v¨¢lida en poliedros convexos al ver que dec¨ªa que se cumpl¨ªa para todos los poliedros limitados por planos.

Como todo resultado matem¨¢tico que pretenda mostrarse como cierto, la f¨®rmula de Euler no tendr¨ªa la validez que se le puede presuponer sin una demostraci¨®n que acredite su certeza. Bien, pues en su trabajo Euler no fue capaz de dar una demostraci¨®n correcta de su f¨®rmula (dio una, pero era incorrecta). Fue Augustin-louis Cauchy quien, en 1811, dio con la primera demostraci¨®n general que se conoce de la f¨®rmula de Euler. Pod¨¦is verla en esta web. Y si os hab¨¦is quedado con ganas de m¨¢s, en este enlace pod¨¦is encontrar nada menos que veinte demostraciones de la validez de la f¨®rmula de Euler.

Antes hemos comentado que Euler fue el primero que habl¨® sobre esta f¨®rmula. Esto es cierto, ya que antes de 1750 no se conoc¨ªa ning¨²n escrito sobre este tema, pero esto no significa que no existiera. De hecho exist¨ªa, pero nadie, salvo Gottfried Wilhelm Leibniz (uno de los fundadores del c¨¢lculo), y quiz¨¢s alg¨²n estudiante m¨¢s, lo sab¨ªa. La cuesti¨®n es que Ren¨¦ Descartes hab¨ªa escrito el, hasta ese momento, primer tratado sobre poliedros, pero muri¨® poco despu¨¦s sin publicarlo.

Tras la muerte de Descartes, parte de sus trabajos (incluido ¨¦ste) fueron trasladados a Francia, y m¨¢s tarde (despu¨¦s de mojarse al caer a un r¨ªo y ser recuperados y secados) llegaron a manos de Leibniz. ?ste se encarg¨® de transcribir algunos de ellos, incluyendo el de poliedros, pero estas transcripciones no vieron la luz hasta 1860, cuando Euler llevaba ya casi 80 a?os fallecido. Esto significa que lo m¨¢s l¨®gico es pensar que ni Euler ni nadie de su ¨¦poca tuvo conocimiento de estos trabajos, por lo que se le consider¨® a ¨¦l como el primero en tratar el tema de los poliedros.

De hecho, actualmente muchos siguen pens¨¢ndolo, ya que la relaci¨®n que hemos comentado de Descartes con los poliedros no es muy conocida. En lo que se refiere al tema protagonista de este art¨ªculo, Descartes lleg¨® a un resultado relacionado con ¨¢ngulos en poliedros a partir del cual es relativamente sencillo deducir la f¨®rmula de Euler, aunque ¨¦l no lleg¨® a deducirla (que se sepa). Los interesados en los detalles de este resultado pueden consultar este enlace.

En un art¨ªculo sobre la f¨®rmula de Euler, no pod¨ªa dejar de comentar la relaci¨®n de este resultado con otro m¨¢s general situado en una rama de las matem¨¢ticas conocida con el nombre de Topolog¨ªa. Con posterioridad al trabajo de Euler, se descubri¨® que la f¨®rmula que lleva su nombre es una generalizaci¨®n de la conocida como caracter¨ªstica de Euler de una superficie (tambi¨¦n conocida como caracter¨ªstica de Euler-Poincar¨¦), que suele denotarse con la letra griega ¦Ö y que pasa por ser un invariante topol¨®gico (esto significa que si dos superficies son topol¨®gicamente iguales, entonces tienen la misma caracter¨ªstica de Euler). En la Wikipedia ten¨¦is una buena introducci¨®n sobre ella.

Y para finalizar, os dejo un poco de entretenimiento. Como sabr¨¦is, los balones de f¨²tbol, aunque son razonablemente esf¨¦ricos, est¨¢n formados en su superficie por pent¨¢gonos y hex¨¢gonos. ?Se podr¨ªa construir un bal¨®n habitual solamente con hex¨¢gonos (no necesariamente regulares)? Y si usamos pent¨¢gonos y hex¨¢gonos, ?cu¨¢ntos de cada tipo deber¨ªamos utilizar para su construcci¨®n? Cuando alguien los haya resuelto en los comentarios pongo los enlaces donde los vi. Y para quien no sepa c¨®mo meterle mano al asunto, quiz¨¢s la f¨®rmula de Euler sea una buena ayuda¡­