El joven de 28 a?os que revolucion¨® los ¡®rayos de luz¡¯

Ayer, 23 de abril, se cumpli¨® el 190 aniversario de la teor¨ªa de los sistemas de rayos, uno de los grandes tratados de la ¨®ptica propuesto por Sir W.R. Hamilton, f¨ªsico y matem¨¢tico irland¨¦s, que con solo 28 a?os se consolid¨® como el renovador de la teor¨ªa de la luz establecida hasta el siglo XIX. Desde una temprana edad, Hamilton hab¨ªa demostrado una gran destreza para las matem¨¢ticas: dominaba el c¨¢lculo integral y la astronom¨ªa, pod¨ªa predecir eclipses y hab¨ªa le¨ªdo a Newton y a Lagrange. Aun as¨ª, Hamilton tuvo que relegar las ciencias a un segundo plano, porque para acceder a la universidad, al Trinity College en Dubl¨ªn, tuvo que dedicarse el estudio de Humanidades. Antes de su ingreso en la universidad en 1823 comunic¨® a su primo Arthur, por carta, el preludio de sus grandes logros. All¨ª dec¨ªa: ¡°En ¨®ptica, he hecho un descubrimiento muy curioso, al menos as¨ª me lo parece...¡±

M¨¢s informaci¨®n

El dodecaedro maldito

La impredecibilidad humana ayuda a ¡®tumbar¡¯ una teor¨ªa de Einstein

Entre estas ideas que esbozaba a su primo, estaba la descripci¨®n geom¨¦trica de los rayos de luz: ¡°Un rayo debe ser considerado como una l¨ªnea recta o curva por la que se propaga la luz; y un sistema de rayos como una colecci¨®n de tales l¨ªneas, con un origen com¨²n. As¨ª, los rayos que divergen desde un punto luminoso componen un sistema ¨®ptico, y, despu¨¦s que se han reflejado en un espejo, componen otro¡±. Hamilton analizaba c¨®mo se comportan los rayos en diferentes medios: si divergen o convergen, si son paralelos, la relaci¨®n entre el ¨¢ngulo de incidencia y el ¨¢ngulo de refracci¨®n, sus combinaciones en haces, etc. Adem¨¢s, formaliz¨® la din¨¢mica de estos haces de manera global e independiente de la naturaleza del proceso ¨®ptico, de forma que su teor¨ªa pod¨ªa aplicarse posteriormente a otros procesos f¨ªsicos.

Con estos textos, Hamilton renov¨® las concepciones iniciales sobre la ¨®ptica, como las teor¨ªas algebraicas de Malus, un oficial de ingenieros del ej¨¦rcito de Napole¨®n en Egipto que descubri¨® la polarizaci¨®n de la luz y propuso un profundo tratado matem¨¢tico sobre su propagaci¨®n. La dificultad de sus c¨¢lculos y el uso de geometr¨ªa y ¨¢lgebra no trivial inspir¨® a Hamilton para formular un principio que resumiera toda la teor¨ªa de forma mucho m¨¢s compacta y sencilla.

Su idea ¡°abarcaba todo lo descubierto acerca de las formas y posiciones de las l¨ªneas a lo largo de las cuales se propaga la luz¡±, seg¨²n se?alaba Hamilton. Su enunciado fundamental, el ahora conocido como ¡°principio de m¨ªnima acci¨®n¡±, puede resumirse en una frase: ¡°un rayo de luz siempre recorre el camino en que el tiempo de transcurso de un punto a otro es m¨ªnimo¡±.

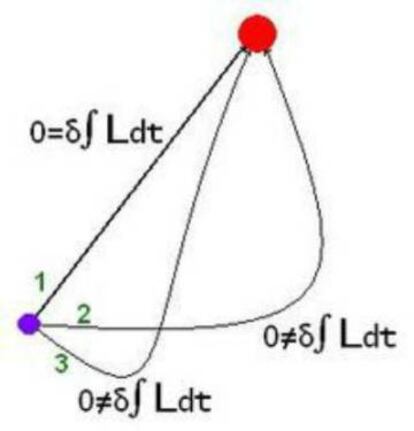
En la figura se ven posibles caminos que podr¨ªa elegir un rayo de luz al propagarse en un medio entre dos puntos. El principio de m¨ªnima acci¨®n dicta, en palabras matem¨¢ticas, que el camino predilecto ser¨¢ la soluci¨®n del llamado problema de puntos cr¨ªticos de un funcional de acci¨®n, es decir, se tratar¨¢ de maximizar o minimizar la integral de una funci¨®n en un intervalo de tiempo cuyos extremos son fijos, denominada funci¨®n Lagrangiana, que depende de las coordenadas del espacio, de las velocidades y del tiempo. Este principio dio lugar a las famosas ecuaciones de Euler-Lagrange de la mec¨¢nica cl¨¢sica, que constituyeron una teor¨ªa equivalente a la mec¨¢nica de Newton, sin necesidad de a?adir t¨¦rminos de fuerza en este formalismo.

Un siglo despu¨¦s, el principio de m¨ªnima acci¨®n se generaliz¨® a la mec¨¢nica cu¨¢ntica y la f¨ªsica at¨®mica, consolidando la teor¨ªa como un marco com¨²n para procesos cl¨¢sicos y cu¨¢nticos. No obstante, Hamilton fue un hombre que siempre concedi¨® poca importancia a sus trabajos, frente a la opini¨®n ajena y com¨²n de que todos sus estudios fueron verdaderas obras maestras, y hasta han sido grabadas en piedra.

Aqu¨ª, seg¨²n caminaba Sir Willam Rowan Hamilton un 18 de Octubre de 1846, en un flash de ingenio, descubri¨® la f¨®rmula fundamental multiplicativa de los cuaterniones:

i? = j? = k? = ijk = ?1

y qued¨® inscrita en una piedra de este puente.

Los llamados cuaterniones, ideados por el matem¨¢tico mientras paseaba con su esposa por su Irlanda natal, son una generalizaci¨®n de los n¨²meros reales, similar a la de los n¨²meros complejos pero con tres unidades imaginarias i, j, k, en vez de una. M¨¢s all¨¢ de su importancia en el ¨¢lgebra, estos n¨²meros tienen aplicaciones en f¨ªsica: representan rotaciones en el espacio, se emplean en el electromagnetismo, en la mec¨¢nica cu¨¢ntica y hasta en rob¨®tica.?

Hamilton fue un hombre verdaderamente entregado a la ciencia, sin ¨¢nimo de celebraci¨®n soberbia de sus triunfos. Y as¨ª lo constat¨® finalmente: ¡°Desde hace mucho tiempo he admirado la descripci¨®n que hace Ptolomeo de su gran maestro astron¨®mico Hiparco, como un hombre que am¨® el trabajo y que am¨® la verdad. Ser¨¢ mi epitafio¡±.

Cristina Sard¨®n es investigadora postdoctoral Severo Ochoa en el ICMAT.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.