D¨¢ndole vueltas al infinito
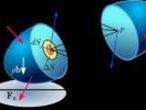
La Paradoja de Banach-Tarski dice que es posible duplicar naranjas mediante giros

Las matem¨¢ticas est¨¢n llenas de sorpresas. Uno de los resultados m¨¢s incre¨ªbles se conoce como la paradoja de Banach-Tarski. Dice que una naranja se puede descomponer en un n¨²mero finito de piezas, de manera que gir¨¢ndolas en el espacio y volvi¨¦ndolas a unir se obtienen dos naranjas id¨¦nticas a la naranja de partida. Es comprensible que esta afirmaci¨®n, aun siendo cierta (e in¨²til para nuestros agricultores) se asocie con la palabra paradoja. Por ejemplo, parece contradecir los m¨¦todos basados en la geometr¨ªa griega donde, para calcular el ¨¢rea de una figura plana, se descompone en varias piezas que se giran y trasladan y, finalmente, se vuelven a unir. De esta forma, se llega a una figura m¨¢s simple (un rect¨¢ngulo, por ejemplo) cuya ¨¢rea s¨ª es conocida. En nuestro caso, este m¨¦todo (cortar la naranja, girar las piezas y volverlas a unir) no se puede aplicar para calcular el volumen de la naranja, ya que llegar¨ªamos a la contradicci¨®n 2=1. Por otra parte, y aunque tambi¨¦n parezca algo extra?o, que un conjunto infinito (y nuestras naranjas matem¨¢ticas est¨¢n compuestas por infinitos puntos) contenga dos copias de s¨ª mismo es algo razonable. Por ejemplo, hay tantos n¨²meros pares o impares como n¨²meros enteros. Lo realmente excepcional de la paradoja de Banach-Tarski es que las dos copias se consiguen solo mediante giros, sin comprimir ni dilatar la naranja de partida.
Para entender c¨®mo se llega a un resultado tan opuesto a la intuici¨®n hay que remontarse al principio del siglo pasado. La investigaci¨®n del matem¨¢tico franc¨¦s Henri Lebesgue, uno de los m¨¢s influyentes de su ¨¦poca, le llev¨® a analizar lo que significa medir conjuntos de n¨²meros reales en la recta. Medir consiste en especificar una funci¨®n que asigne a cada conjunto de la recta un n¨²mero no negativo, generalizando la noci¨®n de longitud. Esta medida de Lebesgue cumple varias propiedades intuitivas, entre las que destacan que:
- El segmento que une el 0 y el 1 mide uno;
- La medida de un conjunto no cambia si lo trasladamos; y
- La medida de cualquier uni¨®n posiblemente infinita de conjuntos disjuntos es la suma de las medidas de cada conjunto.
Una vez formalizada esta nueva noci¨®n de medir conjuntos en la recta, el matem¨¢tico italiano Guiseppe Vitali construy¨® un conjunto de n¨²meros reales que, sorprendentemente, no se puede medir con ninguna funci¨®n que cumpla las reglas enumeradas anteriormente. La existencia de conjuntos no medibles en la recta incomod¨® a la comunidad matem¨¢tica, que trat¨® de encontrar una salida relajando las condiciones impuestas a la funci¨®n de medida. Por ejemplo, en lugar de la tercera propiedad, se puede pedir, alternativamente, que
- La medida de cualquier uni¨®n necesariamente finita de conjuntos disjuntos es la suma de las medidas de cada conjunto.
Guiseppe Vitali?construy¨® un conjunto de n¨²meros reales que no se puede medir
Los matem¨¢ticos polacos Stefan Banach y Alfred Tarski?demostraron que con esta noci¨®n alternativa de medida (que tambi¨¦n se puede generalizar al plano y al espacio) todos los subconjuntos de la recta y del plano son medibles. Sin embargo, en tres dimensiones la presencia de conjuntos no medibles es inevitable y las piezas giradas de la naranja mencionadas en la paradoja son ejemplos de ello. Es precisamente este hecho el que evita la contradicci¨®n 2=1 que aparecer¨ªa si pudi¨¦ramos medir el volumen de las piezas. Una diferencia fundamental que se manifiesta en tres dimensiones es que los giros no son conmutativos. Es decir, el orden en que los aplicamos influye en el resultado final. A su vez, los giros en el espacio tienen un comportamiento parad¨®jico similar al descrito al principio en el caso de las naranjas. De hecho, es ese comportamiento el que propicia, a trav¨¦s de su acci¨®n sobre la naranja, el aparente contrasentido. Uno de los cient¨ªficos m¨¢s geniales, John von Neumann, fue quien encontr¨®, en 1929, la propiedad (llamada promediabilidad) que tienen las traslaciones en la recta y los giros en el plano que impide la existencia de descomposiciones parad¨®jicas (como la de la naranja). Los giros en el espacio, en cambio, no son promediables.
Las descomposiciones parad¨®jicas son un concepto transversal en matem¨¢ticas que ha seguido evolucionando y enriqueciendo otras ¨¢reas y contin¨²an siendo un campo de investigaci¨®n muy activo. Esta breve historia nos dice, adem¨¢s, que para llegar a resultados inesperados es fundamental conocer la investigaci¨®n de los matem¨¢ticos que nos preceden. En nuestro caso, fue la necesidad de entender el significado de medir conjuntos de n¨²meros reales lo que llev¨®, finalmente, a la paradoja de Banach-Tarski.
Fernando Lled¨® es profesor del Departamento de Matem¨¢ticas de la Universidad Carlos III de Madrid y miembro del ICMAT.
Diego Mart¨ªnez es doctorando de la Universidad Carlos III de Madrid y del ICMAT, as¨ª como becario pre-doctoral del proyecto Severo Ochoa.
Caf¨¦ y Teoremas?es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.