El problema de los besos de las esferas

El problema de los besos de las esferas es una cuesti¨®n que ha interesado a muchos matem¨¢ticos desde hace, al menos, unos 300 a?os. Y en el transcurso de su estudio ha quedado patente lo sencillo que es a veces estudiar un problema en ciertas dimensiones y lo complicado que es hacerlo en otras. Vamos a plantear el problema y a comentar todo lo que se conoce de su soluci¨®n.

El problema, como ya hemos comentado, va de colocar esferas ¡°besando¡± a otra esfera inicial. Entendemos ¡°besar¡± como tocar en un punto a dicha esfera, y pedimos que las esferas que coloquemos se toquen entre ellas en, como mucho, un punto. Adem¨¢s, todas las esferas deben ser iguales (la inicial y las que coloquemos despu¨¦s).

En dimensi¨®n 1, una recta, una esfera es un intervalo. Partiendo por tanto de un intervalo inicial, ?cu¨¢ntas esferas (intervalos) podr¨ªamos colocar ¡°besando¡± a la esfera (al intervalo) inicial?

Sin mucho pensar, creo que est¨¢ claro que s¨®lo podemos colocar dos esferas de este tipo (una a cada lado de la esfera del principio). La situaci¨®n quedar¨ªa como sigue (la roja es la esfera inicial):

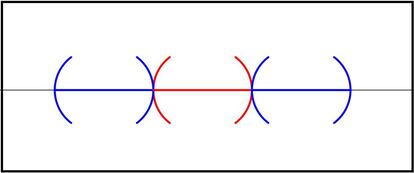
Al n¨²mero de esferas que podemos colocar en cada situaci¨®n se le denomina kissing number (en espa?ol podr¨ªamos llamarlo n¨²mero de osculaci¨®n). Entonces, en el caso de dimensi¨®n uno tenemos que el kissing number es 2.

Pasemos a dimensi¨®n dos, a un plano. En este caso, las esferas son las circunferencias de toda la vida. Colocamos, por tanto, una circunferencia, y despu¨¦s colocamos circunferencias iguales a ¨¦sta ¡°besando¡± (tocando en un ¨²nico punto) a la inicial y toc¨¢ndose, como mucho, en un ¨²nico punto entre ellas. ?Cu¨¢ntas podr¨ªamos colocar en este caso?

Es algo m¨¢s complicado que el anterior, pero tampoco parece demasiado dif¨ªcil concluir que en este caso son seis esferas las que podemos colocar ¡°besando¡± a la inicial. La cosa quedar¨ªa tal que as¨ª (la inicial es la coloreada en rojo):

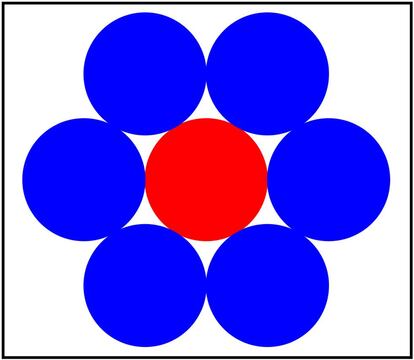
Por tanto, en dimensi¨®n dos el kissing number es 6.

Llegamos ahora al espacio. En este caso, en dimensi¨®n tres, una esfera es lo que todos entendemos cuando escuchamos la palabra esfera: una pelota. Hacemos lo mismo que antes: tenemos una esfera inicial (que, de nuevo, colorearemos de rojo) y colocamos esferas iguales que ellas ¡°besando¡± a esta esfera inicial (de nuevo, estas esferas s¨®lo pueden tocarse, como mucho, en un ¨²nico punto). Antes de seguir leyendo, os invito a que pens¨¦is en ello: ?cu¨¢ntas esferas cre¨¦is que podr¨¦is colocar ¡°besando¡± a la inicial?

En dimensiones uno y dos el problema es bastante sencillo, pero en dimensi¨®n tres la cosa comienza a complicarse. Si uno se mete en el problema, ve que no es demasiado complicado colocar 12 esferas ¡°besando¡± a la inicial, pero seguro que aprecia que queda una nada despreciable cantidad de huecos entre ellas. Estos huecos invitan a pensar que, mediante una recolocaci¨®n de estas 12 esferas, podr¨ªamos dejar espacio para colocar una m¨¢s, con lo que tendr¨ªamos 13 esferas ¡°besando¡± a la esfera inicial.

Newton y Gregory discutieron sobre si el kissing number en dimensi¨®n 3 era 12 ¨® 13. Su disputa no se resolvi¨® hasta casi 300 a?os despu¨¦s

Este asunto fue objeto de disputa entre el gran Isaac Newton y el tambi¨¦n matem¨¢tico brit¨¢nico David Gregory a finales del siglo XVII. La cuesti¨®n le hab¨ªa surgido a Newton a ra¨ªz de unos estudios sobre mec¨¢nica celeste, y conjetur¨® que ser¨ªa 12 las esferas que podr¨ªamos colocar. Sin embargo, David Gregory apoyaba la idea de que los huecos que dejan esas 12 esferas podr¨ªan dejar espacio para una m¨¢s, con lo que ser¨ªan por tanto 13 esferas.

?Pens¨¢is que ser¨¢n 12 o, por el contrario, podremos colocar 13? Quiz¨¢s algunos (o muchos) ve¨¢is que el problema tampoco es demasiado dif¨ªcil, pero la realidad es que este paso a la tercera dimensi¨®n result¨® mucho m¨¢s complicado de lo que pueda parecer. Tanto es as¨ª que la cuesti¨®n no se resolvi¨® hasta 1953, cuando Sch¨¹tte y van der Waerden demostraron que el kissing number en dimensi¨®n 3 es 12, por lo que casi 300 a?os despu¨¦s Newton sal¨ªa vencedor de la disputa contra Gregory (a finales del siglo XIX se presentaron algunas pruebas de este hecho, pero no eran totalmente correctas). En las siguientes im¨¢genes pod¨¦is ver una posible disposici¨®n en la que las esferas que ¡°besan¡± a la inicial (que, como antes, est¨¢ coloreada en rojo) tienen sus centros en los v¨¦rtices de un icosaedro regular cuyo centro es tambi¨¦n el centro de la esfera inicial:

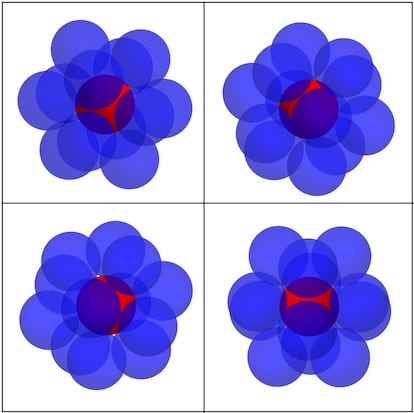
Si llamamos k(n) al kissing number en dimensi¨®n n, tenemos por ahora que k(1)=2, k(2)=6 y k(3)=12. Aunque para dimensiones superiores ya no tendremos im¨¢genes descriptivas del problema (por razones evidentes), tiene mucho sentido preguntarse c¨®mo es el kissing number para n mayor que 3. Bien, pues si ya en dimensi¨®n 3 la cosa era compleja, para dimensiones superiores a¨²n m¨¢s. De hecho, para n mayor que 3 s¨®lo se conoce el kissing number para las dimensiones 4, 8 y 24. Concretamente, tenemos que k(4)=24, k(8)=240 y k(24)=196560. El caso n=4 lo resolvi¨® Oleg Musin en 2003 en su trabajo The kissing number in four dimensions, y los casos n=8 y n=24 fueron resueltos por Henry Cohn y Abhinav Kumar en 2004. Pod¨¦is consultar Optimality and uniqueness of the Leech Lattice among lattices si est¨¢is interesados en el tema.

Del resto de valores de n tenemos, como mucho, cotas del kissing number. Por poner algunos ejemplos, para n=5 sabemos que est¨¢ entre 40 y 44; para n=6 se sabe que est¨¢ entre 72 y 78; para n=7 se encuentra entre 126 y 134; y para n=9 entre 306 y 364. Veremos si en los pr¨®ximos tiempos se concreta alguno de estos valores, estaremos atentos a ello. Mientras tanto, pod¨¦is leer m¨¢s datos sobre el problema del kissing number en Kissing Numbers, Sphere Packings and Some Unexpected Proofs, de Florian Pfender y G¨¹nter M. Ziegler

Es curioso c¨®mo un problema de enunciado tan sencillo puede ser tan f¨¢cil de resolver en algunos casos y tan complicado de demostrar en otros. Y no es, ni mucho menos, el ¨²nico caso. Hay muchos otros problemas de enunciado simple y de sencilla exploraci¨®n en casos peque?os que se complica enormemente cuando subimos de nivel. Hablaremos de otros casos en pr¨®ximos art¨ªculos, pero ser¨ªa interesante que propong¨¢is los casos que conozc¨¢is en los comentarios.