La soluci¨®n al desaf¨ªo matem¨¢tico de la Loter¨ªa de Navidad 2017
Adolfo Quir¨®s Graci¨¢n, profesor de la Universidad Aut¨®noma de Madrid, resuelve el problema planteado a los lectores de EL PA?S
Ya hay soluci¨®n para el desaf¨ªo matem¨¢tico extraordinario de Navidad presentado por EL PA?S y la Real Sociedad Matem¨¢tica Espa?ola?con motivo del sorteo de la loter¨ªa. Adolfo Quir¨®s Graci¨¢n, profesor de la Universidad Aut¨®noma de Madrid?y director de La Gaceta de la RSME present¨® el desaf¨ªo y nos da ahora la soluci¨®n.?
V¨ªdeo | El planteamiento del desaf¨ªo
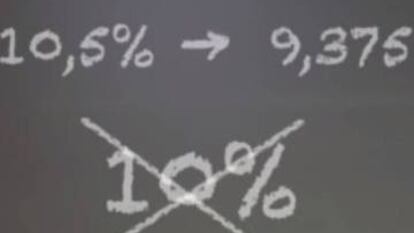
Recordemos que el desaf¨ªo consist¨ªa en, o bien encontrar una sucesi¨®n de resultados (gano o no gano) en los sorteos de loter¨ªa en la que haya podido pasar del 10,5% de "¨¦xito" al 9,375% sin haber estado nunca en el 10%, o bien demostrar que eso no es posible, y que necesariamente debo haber ca¨ªdo por el camino en el 10%.?
Hay muchos "porcentajes de acierto" evitables. Por ejemplo, el 40%. Si gan¨¦ en uno de los dos primeros sorteos y perd¨ª en el tercero, habr¨¦ bajado del 50% al 33,3% sin pasar por ninguno de los porcentajes intermedios.?
Pero el 10% no se puede evitar. Veamos por qu¨¦. Supongamos que 10% fuese evitable y miremos el momento en el que saltamos por encima del 10%. Justo antes habremos jugado J veces, de las que habremos ganado G, y estamos por encima del 10%. En el siguiente sorteo perdemos, y bajamos del 10%.?
Teniendo en cuenta que 10%=1/10, esto significa que G/J > 1/10 > G/(J+1)?
"Multiplicando en cruz", la primera desigualdad es equivalente a?
10 G > J, o 10 G - J >0,?
y la segunda a?
J+1 > 10 G, o 1> 10 G -J.?
Poni¨¦ndolas juntas, 1 > 10 G - J > 0.?
?Pero no hay ning¨²n entero estrictamente entre 1 y 0!?
Por tanto, al pasar del 10,5% al 9,375% necesariamente debemos haber estado en alg¨²n momento en el 10%.?
Del mismo modo pod¨¦is ver que ninguna proporci¨®n que se pueda escribir como 1/N se puede evitar en una reducci¨®n del porcentaje de acierto. Se puede demostrar que todas las dem¨¢s s¨ª son evitables, pero es un poco m¨¢s dif¨ªcil.?
Si los porcentajes en lugar de bajar subiesen, la respuesta ser¨ªa otra: si pierdo en el primer sorteo y gano en el segundo, paso del 0% al 50%, salt¨¢ndome el 10% y muchos otros porcentajes. De hecho, este desaf¨ªo est¨¢ inspirado en otro, propuesto por Adri¨¢n Paenza, en el que los porcentajes, que eran de aciertos en lanzamientos jugando al baloncesto, crec¨ªan en lugar de bajar. Animamos a los lectores a buscar qu¨¦ porcentajes son entonces inevitables.?
Se han recibido dentro del plazo casi 400 respuestas. Aunque no siempre dicen desde donde escriben, las hay procedentes de todas las Comunidades Aut¨®nomas, de una de las Ciudades Aut¨®nomas y de al menos otros nueve pa¨ªses de Am¨¦rica y Europa. Nos alegra constatar que un buen n¨²mero de las soluciones son de j¨®venes estudiantes de ESO o Bachillerato.?
Aproximadamente un 12% del total proponen, o argumentan que existe, una sucesi¨®n de ¨¦xitos y fracasos que evita el 10%. No es un despiste sorprendente, ya que la intuici¨®n nos dice que, al no ser los cambios en los porcentajes continuos, podemos evitar uno dado, sin que se perciba que el 10% tiene algo "especial". Confieso que cuando conoc¨ª el desaf¨ªo de Paenza yo tambi¨¦n empec¨¦ por buscar un ejemplo, y s¨®lo tras varios intentos fallidos cambi¨¦ de estrategia. (Nota: las pocas personas que han contado como ¨¦xitos separados el ganar dos o m¨¢s premios en un mismo sorteo han obtenido, en general, respuestas correctas, pero a un problema distinto al que se planteaba).?
No podemos considerar completas un 18% adicional de las soluciones ya que, aunque dicen que no se puede evitar el 10%, o bien lo hacen bas¨¢ndose s¨®lo en alg¨²n ejemplo o bien dan una explicaci¨®n tan general que se aplicar¨ªa tambi¨¦n al 40%, porcentaje que sabemos que se puede evitar.?
El restante 70% son respuestas correctas de dos tipos. Por un lado, quienes se han dado cuenta de que los porcentajes inicial y final son irrelevantes (algunos incluso observan que no se pueden evitar las fracciones de la forma 1/N), y dan demostraciones m¨¢s o menos parecidas a nuestra soluci¨®n, aunque quiz¨¢s con otro lenguaje (por ejemplo, Juan Vicente S. G. combina geometr¨ªa y probabilidad). Por otro, quienes cubren todas las posibilidades de ir de (m¨²ltiplos) de 21/200 a (m¨²ltiplos de) 3/32 y muestran que en ning¨²n caso es posible evitar pasar por (m¨²ltiplos) de 1/10. De estos ¨²ltimos, unos lo hacen analizando cuidadosamente c¨®mo cambian el numerador y el numerador, como han hecho M.? Jos¨¦ E. M. o Carlos L.-K. A., ?quien nos lo cuenta en forma de f¨¢bula!; otros, m¨¢s formales, utilizan sucesiones, como ha hecho por ejemplo Javier S. M.; algunos dan demostraciones geom¨¦tricas, en ocasiones muy elegantes, como las de Juan S. A. o ?ngela V.??
La RSME ha decidido enviar un ejemplar del libro de Martin Erickson Soluciones ?Aj¨¢!, que forma parte de la Biblioteca Est¨ªmulos Matem¨¢ticos que publica conjuntamente con Editorial SM, a tres lectores seleccionados por la sociedad. Son Isabel O. A., Juan Manuel C. M. y F¨¦lix M. P.?
Hay¨¢is dado o no con la respuesta, espero que el desaf¨ªo os haya resultado interesante. En nombre de EL PA?S, de la RSME y en el m¨ªo propio, os deseo felices fiestas ?y suerte con la loter¨ªa!
Mira todos los desaf¨ªos anteriores
TODA LA INFORMACI?N SOBRE LA LOTER?A DE NAVIDAD

Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.

































































