Un cuadrado triangulado de una forma muy especial

Hoy vamos a hablar sobre triangulaciones de un cuadrado, es decir, de dividir un cuadrado en tri¨¢ngulos. En este blog ya hemos hablado sobre triangulaciones de pol¨ªgonos, concretamente en Tetraedrizando, que es gerundio, pero en este caso vamos a profundizar un poco m¨¢s estudiando unas muy concretas.

Lo que queremos es triangular un cuadrado de forma que todos los tri¨¢ngulos que nos queden tengan exactamente la misma ¨¢rea. En aquel momento, no nos preocupamos por el ¨¢rea de los tri¨¢ngulos, pero ahora queremos que todas las ¨¢reas sean exactamente iguales.

Imaginemos que queremos dividir un cuadrado en n tri¨¢ngulos con la misma ¨¢rea. Hay una forma sencilla de hacer esto:

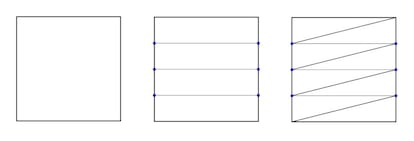
- Dividimos dos lados opuestos del cuadrado, por ejemplo los verticales, en n/2 segmentos de la misma longitud.

- Unimos los puntos que queden a la misma altura con segmentos. Nos queda n/2 rect¨¢ngulos iguales.

- Dividimos cada rect¨¢ngulo en dos tri¨¢ngulos trazando una de las diagonales. Obtenemos as¨ª n/2 tri¨¢ngulos de la misma ¨¢rea.

En la siguiente imagen pod¨¦is ver un ejemplo en el que hemos dividido el cuadrado inicial en 8 tri¨¢ngulos de la misma ¨¢rea:

Problema resuelto, ?verdad? Pues s¨ª y no. Con este procedimiento podemos hacer la triangulaci¨®n que quer¨ªamos, pero si os fij¨¢is obtendremos siempre un n¨²mero par de tri¨¢ngulos. La pregunta realmente interesante en este asunto es la siguiente: ?podemos triangular un cuadrado de manera que nos quede un n¨²mero impar de tri¨¢ngulos de la misma ¨¢rea? Pod¨¦is pensar en ello antes de seguir leyendo, por ejemplo buscando una triangulaci¨®n con tres tri¨¢ngulos (el caso m¨¢s simple en teor¨ªa), a ver si se os ocurre alguna manera de hacerlo.

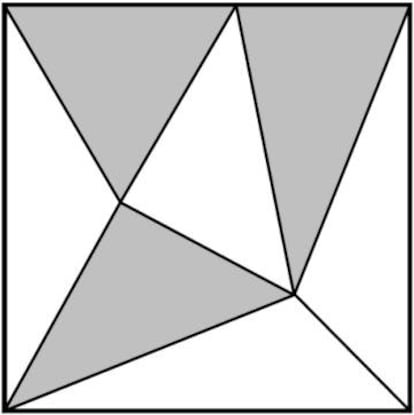
Tened en cuenta una cosa: los tri¨¢ngulos tienen que tener la misma ¨¢rea, pero no hace falta que sean exactamente iguales en forma. En la imagen pod¨¦is ver una posible triangulaci¨®n impar¡­que, por desgracia, es incorrecta, ya que en realidad no todos los tri¨¢ngulos tienen la misma ¨¢rea (por poco).

Adentr¨¦monos un poco m¨¢s en el tema. Sorprendentemente, la primera referencia de alguien que se pregunt¨® si un cuadrado pose¨ªa una triangulaci¨®n impar fue Fred Richman en 1965. Y decimos sorprendentemente porque esta cuesti¨®n tiene pinta de problema que podr¨ªa haberse estudiado en la Grecia cl¨¢sica. El caso es que, a partir de esto, un compa?ero de Richman, John Thomas, consigui¨® demostrar que no existen triangulaciones impares si las coordenadas de los v¨¦rtices de los tri¨¢ngulos ten¨ªan ciertas caracter¨ªsticas (m¨¢s concretamente, si eran todas racionales con denominador impar).

Thomas envi¨® su trabajo a una publicaci¨®n, y el revisor le dijo que ten¨ªa pinta de ser una cuesti¨®n sencilla y muy estudiada, por lo que le propuso que lo mandara en forma de problema para los lectores y que, si en un tiempo no lo hab¨ªan resuelto, se lo publicar¨ªan. Y eso teniendo en cuenta que dicho revisor no consigui¨® demostrar por s¨ª mismo el resultado de Thomas y tampoco consigui¨® encontrar ninguna referencia anterior al mismo. ?Qu¨¦ acab¨® ocurriendo? Que se public¨® unos a?os despu¨¦s, en 1968.

Pero esto no resolv¨ªa el problema, segu¨ªamos sin saber si existen triangulaciones impares de un cuadrado en el caso general¡­hasta 1970. En ese a?o, Paul Monsky demostraba el caso general a partir del trabajo del propio Thomas. Os presento el teorema de Monsky:

No es posible dividir un cuadrado en un n¨²mero impar de tri¨¢ngulos de la misma ¨¢rea.

Para demostrar esto, Monsky utiliz¨® de manera muy inteligente ciertas herramientas algebraicas (s¨ª, algebraicas) y un bonito resultado conocido como lema de Sperner, que podemos enunciar de la siguiente forma:

Toma un tri¨¢ngulo cualquiera y numera los v¨¦rtices con los n¨²meros 1, 2 y 3. Ahora divide el tri¨¢ngulo en triangulitos m¨¢s peque?os, los que quieras y como quieras, pero cuid¨¢ndote de que dos lados de los tri¨¢ngulos interiores o no se toquen o se toquen en un v¨¦rtice. Los nuevos v¨¦rtices que hayan aparecido entre el 1 y el 2 del inicial num¨¦ralos con unos o doses a tu gusto; los que hayan aparecido entre el 1 y el 3 del inicial num¨¦ralos con unos o treses, tambi¨¦n como prefieras; y lo mismo con los que haya entre el 2 y el 3 del inicial, ponle doses o treses como te apetezca. A los v¨¦rtices que hayan surgido dentro del tri¨¢ngulo ponle unos, doses o treses a tu antojo.

Entonces, seguro que habr¨¢ al menos un triangulito peque?o cuyos v¨¦rtices est¨¦n numerados como el inicial, con un 1, un 2 y un 3. De hecho, el n¨²mero de triangulitos que cumple esto es impar.

Os invito a que hag¨¢is vosotros el dibujo del tri¨¢ngulo, la divisi¨®n en triangulitos y la numeraci¨®n de v¨¦rtices para que lo ve¨¢is con vuestros propios ojos.

Los interesados en ver la demostraci¨®n completa del teorema pueden consultar el propio trabajo de Monsky, On Dividing a Square into triangles. Y quienes quieran ampliar informaci¨®n sobre este tema tambi¨¦n pueden leer Cutting a Polygon into Triangles of Equal Areas, de Sherman Stein, y One square and an odd number of triangles, de M. Aigner y G. M. Ziegler. En ellos, adem¨¢s de la demostraci¨®n de Monsky, podr¨¦is ver generalizaciones del problema a otros pol¨ªgonos y tambi¨¦n a tres dimensiones.

Y para terminar, un detalle: hasta donde yo s¨¦, no se conoce ninguna otra demostraci¨®n de la no existencia de triangulaciones impares de un cuadrado aparte de la de Monsky. Si alguien tiene m¨¢s informaci¨®n al respecto, estaremos encantados de que nos hable sobre ello en los comentarios.