Mersenne y las m¨¢quinas para fabricar n¨²meros primos

Hoy en d¨ªa, la seguridad en las comunicaciones a trav¨¦s de internet, y otras tecnolog¨ªas, requieren para su funcionamiento encontrar n¨²meros primos de gran cantidad de cifras. Pero m¨¢s all¨¢ de los ordenadores, la caza de primos, cantidades ¨²nicamente divisibles entre s¨ª mismas y la unidad, ha sido uno de los desaf¨ªos matem¨¢ticos que m¨¢s pasiones ha levantado a lo largo de la historia. Euclides, en torno al 300 antes de Cristo, ya relacion¨® los llamados n¨²meros perfectos, que son iguales a la suma de sus divisores propios (como el 6; 6 = 1 + 2 + 3), con n¨²meros primos de la forma 2^p - 1 (siendo p un n¨²mero primo).

Unos cuantos siglos despu¨¦s, esta misma expresi¨®n fue propuesta por el fil¨®sofo, matem¨¢tico y sacerdote franc¨¦s Marin Mersenne (1588-1648) con el objetivo de producir n¨²meros primos. Mersenne, que falleci¨® hace 370 a?os un 1 de septiembre, estudi¨® teolog¨ªa, matem¨¢ticas y teor¨ªa musical. Tras intentar, sin ¨¦xito, hallar una f¨®rmula que describiera a todos los primos, se dedic¨® a estudiar la expresi¨®n M(n) = 2^n - 1, con n un n¨²mero natural. Aunque no produce primos para cualquier valor de n (de hecho, cuando n es compuesto, M(n) siempre es compuesto), de forma bastante recurrente s¨ª lo hace. Los n¨²meros primos que se pueden expresar de esta manera se llaman primos de Mersenne. En 1641, Mersenne enunci¨® en su obra Cogitata physico-mathematica que cuando n es un primo menor o igual que 257, solo los n¨²meros M(2), M(3), M(5), M(7), M(13), M(17), M(19), M(31), M(67), M(127) y M(257) eran primos. Sin embargo, esta lista no era correcta: M(67) y M(257) son en realidad compuestos, mientras que faltan los primos M(61), M(89) y M(107).

Se ha especulado mucho sobre el m¨¦todo que sigui¨® Mersenne para escoger su lista y parece que consider¨® que M(p) era primo siempre que p se pudiera escribir como 2^k + 1, 2^k - 1, 4^k + 3 o 4^k - 3 (siendo k un n¨²mero natural), y viceversa. Sin embargo, este criterio no explicaba la omisi¨®n del caso M(61), que lo cumple para k = 3 (61 = 4^3 - 3). Esto podr¨ªa deberse a que Mersenne crey¨® err¨®neamente que era compuesto, o m¨¢s probablemente a un error tipogr¨¢fico a la hora de escribir la lista.

La b¨²squeda de una explicaci¨®n para la lista de Mersenne llev¨® a la llamada nueva conjetura de Mersenne, que sostiene que si dos de las tres condiciones siguientes son ciertas, tambi¨¦n lo es la tercera: 1) M(p) es primo; 2) p = 2^k + 1; 2^k - 1; 4^k + 3 o 4^k - 3; 3) (2^p + 1) / 3 es primo. Hoy en d¨ªa se contin¨²a el estudio de esta conjetura con ayuda de ordenadores. Tambi¨¦n se emplea la capacidad de c¨¢lculo de los ordenadores para encontrar primos de Mersenne cada vez m¨¢s grandes. Hasta la fecha se conocen 50, siendo el mayor M(77232917), con m¨¢s de 23 millones de cifras. Sin embargo, no se sabe si, tal y como le ocurri¨® a Mersenne, se est¨¢ omitiendo alg¨²n primo m¨¢s peque?o por el camino.

A lo largo de la historia se han empleado otras f¨®rmulas para generar primos. En 1772, Leonhard Euler observ¨® que la expresi¨®n P(n) = n^2 + n + 41 generaba primos para n = 0, 1, 2, ¡­, 39, pero a partir de 40 comienzan a aparecer tambi¨¦n n¨²meros compuestos. Estas expresiones polin¨®micas son m¨¢s simples de manejar que las que involucran potencias, como la de Mersenne, pero su potencia es limitada, ya que ning¨²n polinomio P(n) con coeficientes enteros genera primos para todos los valores de n.

Considerando polinomios con m¨¢s variables, del tipo P(x, y)= 2x^2 +3xy + y^7 +8, se obtienen f¨®rmulas sorprendentes, como la que se desprende del famoso teorema de Matiyasevich en el que da la soluci¨®n a uno de los problemas planteados por Hilbert sobre ecuaciones diof¨¢nticas. En 1976 un grupo de matem¨¢ticos emple¨® este teorema para afirmar que los valores positivos de la expresi¨®n que aparece en la imagen de abajo son todos los primos. Pero comprobar esto de forma efectiva es una tarea impracticable, ya que dando valores de 0 a infinito a las variables, en su inmensa mayor¨ªa se obtienen n¨²meros negativos.

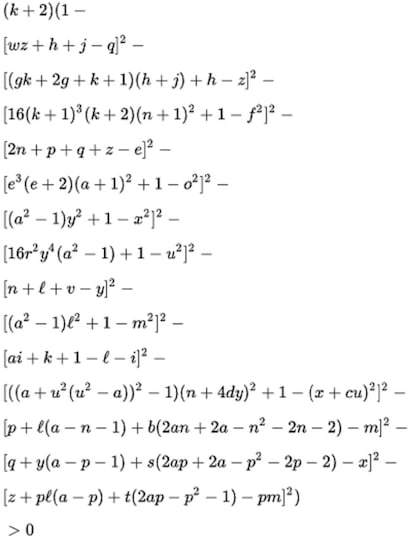
?Podr¨ªa haber entonces alguna f¨®rmula sencilla que los generara todos, como pretend¨ªa Mersenne? Existen algunas que rastrean los n¨²meros naturales y localizan autom¨¢ticamente los n¨²meros primos. Por ejemplo, la f¨®rmula de Wilson que aparece en la segunda imagen genera para cada n el valor n + 1 si n + 1 es primo y el valor 2 si no lo es. Aunque es mucho m¨¢s sencilla que la f¨®rmula anterior, resulta poco pr¨¢ctica, ya que su coste de c¨¢lculo es muy elevado. En general, cuantos m¨¢s casos contemplan (m¨¢s n¨²meros primos producen) las f¨®rmulas, m¨¢s ineficientes computacionalmente resultan. As¨ª que por el momento, seguiremos buscando una m¨¢quina m¨¢s eficiente que ayude a generar primos.

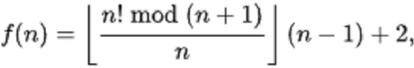
Jos¨¦ Granados es estudiante de doctorado en matem¨¢ticas de la Universidad Aut¨®noma de Madrid y miembro del ICMAT.

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT)

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".