?Hablan las c¨¦lulas el lenguaje de las matem¨¢ticas?

Tanto durante el desarrollo embrionario como en el individuo adulto, las c¨¦lulas necesitan saber d¨®nde est¨¢n, cu¨¢ntas son, con qu¨¦ otras tienen que interactuar y cu¨¢nto tienen que proliferar para formar tejidos diferentes de tama?o y forma concretos. Esto requiere que conversen entre ellas, a trav¨¦s de la comunicaci¨®n celular, que no es m¨¢s que la capacidad que tienen todas las c¨¦lulas de intercambiar informaci¨®n fisicoqu¨ªmica con el medio ambiente y con otras c¨¦lulas para poder actuar coordinadamente. Sin embargo, a¨²n existen muchos interrogantes sobre este proceso: ?c¨®mo es la comunicaci¨®n entre c¨¦lulas adyacentes o alejadas? ?C¨®mo se emiten, reciben e interpretan las se?ales moleculares en esta comunicaci¨®n? ?Est¨¢n estas se?ales orientadas y dirigidas hacia c¨¦lulas m¨¢s predispuestas a su recepci¨®n? Y la pregunta m¨¢s importante, ?c¨®mo podemos influir en este proceso de comunicaci¨®n? Las matem¨¢ticas son una herramienta esencial para responder a estas cuestiones de inter¨¦s biol¨®gico.

En 1952 el matem¨¢tico ingl¨¦s Alan Turing sent¨® las bases de la modelizaci¨®n matem¨¢tica de la morfog¨¦nesis. Durante este proceso la comunicaci¨®n celular es fundamental, ya que es a trav¨¦s de se?ales c¨®mo se controlan los c¨®digos gen¨¦ticos que hacen que la c¨¦lula modifique su comportamiento, o incluso su misma esencia, para construir o dise?ar un patr¨®n determinado (forma, tama?o, diferenciaci¨®n tisular, etc.). Turing atribuy¨® la formaci¨®n de patrones a mecanismos de difusi¨®n de estas se?ales (en concreto, al movimiento aleatorio de las se?ales, que aparece como resultado de interacciones con las mol¨¦culas del fluido extracelular) junto a procesos de reacci¨®n qu¨ªmica entre ellas (activaci¨®n o represi¨®n de la se?al) en el entorno que rodea a las c¨¦lulas.

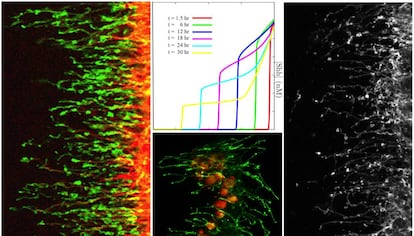
En esta ¨²ltima d¨¦cada, el enorme avance de las t¨¦cnicas de microscop¨ªa y el desarrollo de herramientas moleculares permitieron seguir con m¨¢s detalle la din¨¢mica de estas se?ales, y gracias a ello se pudo observar una realidad bien diferente a la intuida por Turing. El conocimiento actual nos lleva a considerar que las c¨¦lulas se comunican por contacto directo incluso cuando se encuentran muy alejadas entre s¨ª. El proceso de transferencia de se?ales se lleva a cabo mediante extensiones retr¨¢ctiles de la membrana celular (denominadas filopodios o nanotubos). La informaci¨®n bioqu¨ªmica a transmitir circula por estas estructuras, como ocurre durante la comunicaci¨®n neuronal, en lo que parece ser un sistema gen¨¦rico de comunicaci¨®n.

La c¨¦lula receptora interpreta estas se?ales mediante las denominadas rutas de se?alizaci¨®n, a las que se asocian determinadas mol¨¦culas que act¨²an desde el inicio del est¨ªmulo para que las c¨¦lulas respondan. Estas rutas son espec¨ªficas para cada se?al y cada una regula la expresi¨®n de unos genes concretos. Entre ellas, la ruta de Hedgehog-Gli, en la que centramos nuestra investigaci¨®n, es fundamental durante el desarrollo animal y en el crecimiento tumoral. En este proceso est¨¢n involucrados aspectos puramente mec¨¢nicos (la din¨¢mica de elongaci¨®n y retracci¨®n de filopodios, los factores responsables del direccionamiento de la informaci¨®n, etc.) y aspectos moleculares, cuyo resultado perfectamente coordinado no da opci¨®n a la aleatoriedad.

Todo este perfecto engranaje puede ser modelado por ecuaciones diferenciales en las diversas escalas del proceso (los tiempos de transmisi¨®n de la se?al y de reacci¨®n de la c¨¦lula son diferentes, al igual que el recorrido espacial de la se?al fuera y dentro de la c¨¦lula), que permiten predecir y aprender de su din¨¢mica. Los modelos matem¨¢ticos en biolog¨ªa ayudan a revelar nuevos fen¨®menos, din¨¢micas no esperadas o patrones evolutivos, para formular y corroborar nuevos experimentos, y a direccionarlos en la b¨²squeda de respuestas.

Prototipos

En este caso, el conocimiento b¨¢sico de lo micro o lo nano nos posibilita establecer prototipos y trasladarlos a una escala macrosc¨®pica, la del tejido o tumor. Con estos m¨¦todos podemos saber c¨®mo se orientan los filopodios que median la se?alizaci¨®n celular, c¨®mo de espec¨ªfico es el proceso en cada tipo de se?al y la posibilidad de que comportamientos celulares o moleculares individuales deriven en un comportamiento colectivo. Con intereses terap¨¦uticos, esta modelizaci¨®n es clave para sentar los principios para la identificaci¨®n de nuevos inhibidores o promotores de estas rutas de se?alizaci¨®n que cuando est¨¢n alteradas son causantes de patolog¨ªas.

De esta manera, desarrollos matem¨¢ticos, como la teor¨ªa del potencial o las integrales singulares, las ecuaciones diferenciales aplicadas a transporte sobre filamentos, el c¨¢lculo de variaciones o las propiedades de dispersi¨®n de flujos saturados, se unen a los avances en microscop¨ªa, la comprensi¨®n de los mecanismos moleculares de la se?alizaci¨®n celular basados en la informaci¨®n bioqu¨ªmica y gen¨¦tica, y el estudio del comportamiento celular colectivo. Es apasionante observar el poder de predicci¨®n de las matem¨¢ticas cuando ¨¦stas se asientan en principios biol¨®gicos s¨®lidos, permitiendo caminar por senderos no explorados de la ciencia y liderar nuevos descubrimientos.

Isabel Guerrero es profesora de Investigaci¨®n del CSIC, Centro de Biolog¨ªa Molecular Severo Ochoa. Universidad Aut¨®noma de Madrid.

Juan Soler. Catedr¨¢tico de Matem¨¢tica Aplicada, Universidad de Granada.

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT)

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales, y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".