Matem¨¢ticas para proteger la democracia

La democracia es considerada el sistema pol¨ªtico que m¨¢s voz y poder otorga a los ciudadanos. En palabras del premio Nobel Octavio Paz, ¡°sin democracia, la libertad es una quimera¡±. Sin embargo, a veces esa herramienta puede verse manipulada sin que la ciudadan¨ªa se d¨¦ cuenta. Esto es lo que ocurre a veces con una t¨¦cnica pol¨ªtica conocida como gerrymandering. Pero las matem¨¢ticas permiten detectarlo.

En las elecciones legislativas de Estados Unidos, como las que tuvieron lugar el pasado 6 de noviembre, cada estado se divide en tantos distritos electorales como miembros para la C¨¢mara de Representantes le sean asignados, y cada distrito elige como representante al candidato que obtiene la mayor¨ªa de votos. Cada diez a?os, el gobierno de un estado puede modificar a su antojo el dise?o de esas circunscripciones electorales: esta es la t¨¢ctica del gerrymandering. "Hay casos en los que se ha utilizado para propiciar avances sociales y garantizar la representatividad de minor¨ªas raciales, pero su intenci¨®n habitual es obtener beneficios pol¨ªticos", indica Carmen M¨¦ndez, coordinadora del m¨¢ster de Estudios Americanos de la Universidad Complutense de Madrid.

Aunque el t¨¦rmino gerrymandering se invent¨® en EE. UU., el fen¨®meno tambi¨¦n ¡°puede darse de forma excepcional en otros pa¨ªses como Francia e Italia¡±, indica M¨¦ndez. Sin embargo, en Espa?a no: ¡°Las fronteras de los distritos electorales est¨¢n basadas en un dise?o provincial de la Constituci¨®n de 1978 y no se pueden modificar para las elecciones generales ni para otras votaciones¡±.

En los pa¨ªses en los que se aplica, esta estrategia puede cambiar considerablemente el resultado. Imaginemos un estado compuesto por 25 personas que debe elegir a cinco representantes entre dos partidos: el verde y el azul. El 60 % de la poblaci¨®n vota al verde y, el 40 %, al azul. En la primera imagen, el trazo de los cinco distritos electorales hace que el partido verde obtenga tres representantes y el partido azul dos, siendo el n¨²mero de representantes de cada partido proporcional al voto. Sin embargo, en el segundo dise?o el partido verde se lleva los cinco representantes y en el tercer ejemplo solo dos, a pesar de tener la mayor¨ªa. ¡°El partido en el poder puede beneficiarse del redise?o de las fronteras electorales y conseguir que el voto se concentre a su favor. Los otros partidos y sus votantes salen perjudicados¡±, explica M¨¦ndez.

En situaciones reales es complicado determinar si esta estrategia se ha utilizado de forma fraudulenta. En el ejemplo anterior se observa que el trazado no tiene ni siquiera por qu¨¦ tener una forma sospechosa para favorecer a un partido (como sucede en el segundo gr¨¢fico). ?C¨®mo saberlo entonces? El grupo de matem¨¢ticos Quantifying Gerrymandering de la Universidad de Duke (EE. UU.) ha desarrollado t¨¦cnicas que intentan proteger la democracia. ¡°Utilizando algoritmos de muestreo estad¨ªstico, simulamos miles de posibles mapas con diferentes dibujos de distritos que cumplen criterios de distribuci¨®n neutrales, teniendo en cuenta la geograf¨ªa y las opiniones pol¨ªticas¡±, explica el investigador principal del proyecto, Jonathan Mattingly. Concretamente, ¡°usamos los llamados m¨¦todos de Monte Carlo basados en cadenas de Markov, que fueron desarrollados como parte del proyecto Manhattan¡±, detalla el tambi¨¦n investigador del grupo Gregory Herschlag.

Aplicando a estos mapas las votaciones hist¨®ricas a lo largo de los a?os, obtienen un rango t¨ªpico de resultados electorales que pueden usar para comparar cualquier otro mapa. ¡°Si un cierto dise?o se encuentra en un extremo at¨ªpico del conjunto, podemos concluir que se trata de manipulaci¨®n partidista¡±, aclara Herschlag.

Precisamente, el grupo se encontr¨® con que ¡°los mapas de distritos de Carolina del Norte de las elecciones legislativas de 2012 y 2016 ten¨ªan dentro de nuestra distribuci¨®n valores estad¨ªsticos altamente at¨ªpicos¡±, indica Mattingly. El Partido Dem¨®crata obtuvo, respectivamente, cuatro y tres de los 13 representantes totales, ¡°un resultado que solo se daba en menos del 1% de los mapas simulados¡±. Tambi¨¦n hab¨ªa caracter¨ªsticas sospechosas, como distritos sobrecargados de votantes dem¨®cratas y lo contrario. ¡°Simplemente cambiando el trazado, los dem¨®cratas pod¨ªan pasar a tener nueve representantes; la elecci¨®n variaba enormemente sin modificar ni un solo voto¡±, a?ade el matem¨¢tico. En los comicios de este a?o, el resultado ha vuelto a ser tres contra diez.

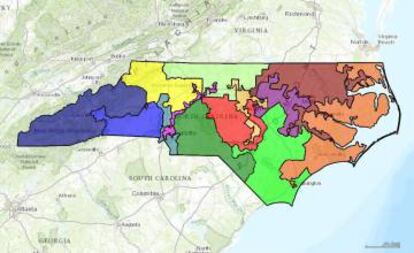
El descubrimiento llev¨® a Mattingly a testificar como experto ante el tribunal de Carolina del Norte en el Common Cause v. Rucho. ¡°Los jueces concluyeron que el caso era extremo e inconstitucional. Ahora est¨¢ por ver si la Corte Suprema de los Estados Unidos comparte este punto de vista¡±, explica Mattingly.

M¨¦ndez afirma que los modelos matem¨¢ticos facilitan determinar si esta pr¨¢ctica deber¨ªa ser legal o no, "ya que en el terreno pol¨ªtico en ocasiones se utiliza una ret¨®rica conectada con lo emocional y los derechos individuales, que dificulta una visi¨®n de conjunto". Los investigadores de Duke lo tienen claro: ¡°Las matem¨¢ticas pueden ayudar a terminar con el gerrymandering porque solo una comprensi¨®n profunda del problema puede hacerlo¡±.?

Juan Jos¨¦ Mar¨ªn es investigador del ICMAT.?Patricia Ruiz Guevara es matem¨¢tica por la Universidad de Murcia y periodista cient¨ªfica.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".