Matem¨¢ticas para responder ante un tsunami

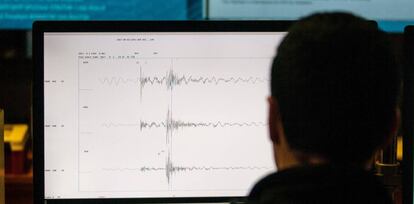
Cada instante, los nodos de la red s¨ªsmica internacional recogen datos de movimiento en el fondo del mar, mientras que miles de boyas, estrat¨¦gicamente situadas, detectan irregularidades en la superficie. Esta informaci¨®n se env¨ªa de forma continua a los centros de alerta, donde se identifican eventos s¨ªsmicos que superan una determinada intensidad y suceden en zonas cr¨ªticas. Cuando as¨ª ocurre, se genera una alerta, y se ponen en marcha los protocolos. Ante el riesgo de tsunami, lo importante es actuar r¨¢pido. Las matem¨¢ticas son clave para predecir la magnitud de la cat¨¢strofe y mitigar, en la medida de lo posible, los da?os.

A los cinco minutos ya se dispone de datos suficientes (al menos, la localizaci¨®n e intensidad del se¨ªsmo) para hacer las primeras simulaciones num¨¦ricas. Los modelos matem¨¢ticos predicen a tiempo real la propagaci¨®n del tren de ondas y el impacto en costa. El modelo escogido en cada centro depender¨¢ del tipo de informaci¨®n que quieran obtener, buscando el mejor equilibrio entre que sea descriptivo, por un lado, y manejable, por el otro. Cuanta m¨¢s precisi¨®n se busque, m¨¢s descripci¨®n f¨ªsica se debe introducir en el modelo.

En un tsunami se dan varios fen¨®menos f¨ªsicos, gobernados por diferentes ecuaciones en derivadas parciales. Una idea general de la altura de las olas o su tiempo de llegada a la costa se puede deducir de las ecuaciones de propagaci¨®n de ondas. Son ecuaciones lineales (las variables no tienen exponentes ni operadores complicados), sencillas de formular y resolver. Sin embargo, para conseguir informaci¨®n m¨¢s refinada es necesario considerar ecuaciones no lineales. Las m¨¢s elementales son las ecuaciones de aguas someras. Fueron propuestas a finales del siglo XIX por el matem¨¢tico e ingeniero franc¨¦s Adh¨¦mar Jean Claude Barr¨¦ de Saint-Venant, quien las obtuvo a partir de las ecuaciones de Navier Stokes (que describen el movimiento de un fluido y cuya resoluci¨®n es uno de los problemas del milenio), simplificando la complejidad.

El sistema de aguas someras es algo m¨¢s sencillo, aunque tenga tambi¨¦n sus dificultades anal¨ªticas. En cualquier caso, para obtener predicciones es preciso realizar aproximaciones num¨¦ricas. Es importante que sean buenas estimaciones pero adem¨¢s, que se puedan calcular (usando t¨¦cnicas de computaci¨®n de alto rendimiento) en un corto periodo de tiempo. Si no se tienen los resultados antes de que llegue la onda, el modelo no servir¨ªa de nada. El grupo EDANYA, en la Universidad de M¨¢laga, ha conseguido realizar una simulaci¨®n real de ocho horas de propagaci¨®n de un tsunami en el Mediterr¨¢neo en 30 segundos. Por ahora, la suya es la mejor soluci¨®n para la modelizaci¨®n de tsunamis.

Este grupo trabaja, entre otros temas, en el dise?o de nuevos modelos para la simulaci¨®n de tsunamis a?adiendo t¨¦rminos adicionales a las ecuaciones de aguas someras, as¨ª como en t¨¦cnicas eficientes para su discretizaci¨®n, que determinan la resoluci¨®n que tendr¨¢ el resultado. ¡°En la propagaci¨®n en medio del oc¨¦ano se pueden usar mallas ¨Cret¨ªculos que se emplean para buscar soluciones aproximadas- de kil¨®metros, pero a medida que la ola se acerque a la costa se necesitar¨¢ mayor resoluci¨®n¡±, explicaba Manuel Castro D¨ªaz, miembro del grupo. Despu¨¦s, el equipo determina c¨®mo implementar de forma eficiente este tipo de algoritmos, usando tarjetas gr¨¢ficas de los ordenadores para reducir el tiempo de c¨®mputo. El resultado es una predicci¨®n precisa (con errores menores al 5% cuando se comparan con datos obtenidos en experimentos de laboratorio) sobre la forma y la altura de las olas en las zonas cercanas a la costa, y de los mapas de inundaci¨®n (es decir, hasta d¨®nde llegar¨¢ la ola en el territorio afectado).

Pero, ?podr¨ªa fallar el modelo, y no obtener soluciones (o no darlas a tiempo)? S¨ª, aunque es poco probable. Por el momento, por si acaso sucede eso, se utilizan bases de soluciones pre calculadas, cat¨¢logos de cientos de miles de eventos que previamente se han simulado. ¡°Es mucha informaci¨®n almacenada y es complicada de procesar, por lo que se generan muchos problemas. Aunque al principio los centros de alerta eran reacios a usar la herramienta de simulaci¨®n a tiempo real, porque es novedosa, cada vez se dan cuenta de que es m¨¢s que suficiente: aporta m¨¢s flexibilidad y precisi¨®n¡±, concluye Castro. Sus modelos ya se emplean en el Centro de Alerta Temprana de Tsunamis, con sedes en Roma y en Pisa, por ejemplo, que vigila las zonas de m¨¢s sismicidad del Mediterr¨¢neo, frente a las costas griegas, en Turqu¨ªa y la costa de Argelia.

M¨¢s all¨¢ de esta aplicaci¨®n, la aproximaci¨®n y simulaci¨®n num¨¦rica del grupo EDANYA se emplea para modelar otros fen¨®menos gobernados por leyes f¨ªsicas parecidas: la din¨¢mica litoral y fluvial; la formaci¨®n de planetas o agujeros negros; el sistema cardiovascular... Los modelos permiten estudiar la evoluci¨®n de los fluidos medioambientales y de salud en todos estos casos, con poco coste y gran precisi¨®n.

?gata Tim¨®n (ICMAT).

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n:?gata Tim¨®n (ICMAT).