Qu¨¦ es la teor¨ªa de categor¨ªas y c¨®mo se ha convertido en tendencia

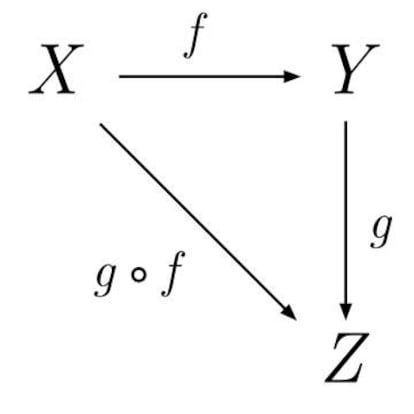
Recientemente, una rama de las matem¨¢ticas llamada teor¨ªa de categor¨ªas ha captado la atenci¨®n de varios medios cient¨ªficos tras ganar bastante popularidad dentro de la comunidad matem¨¢tica en los ¨²ltimos a?os. La situaci¨®n ha llegado al punto en el que algunos matem¨¢ticos se est¨¢n quejando en Twitter de que hay investigadores que tuitean m¨¢s sobre teor¨ªa de categor¨ªas que sobre sus propias especialidades. Pero, ?qu¨¦ es esta rama de las matem¨¢ticas y por qu¨¦ est¨¢ tan de moda?

Algunas personas llaman a la teor¨ªa de categor¨ªas ¡°las matem¨¢ticas de las matem¨¢ticas¡±, ya que se sit¨²a por encima de muchas disciplinas matem¨¢ticas, conect¨¢ndolas. Fue propuesta en 1945 como una herramienta para trasladar problemas matem¨¢ticos de un campo a otro, en el que se pudieran resolver con mayor facilidad. Por ejemplo, sabemos que en cualquier momento debe haber un punto en la superficie de la Tierra donde la velocidad del viento es cero. Pero para demostrar este precioso resultado lo debemos traducir a una afirmaci¨®n algebraica, para lo que es ¨²til emplear una pizca de teor¨ªa de categor¨ªas. Habitualmente, resultados m¨¢s complejos requieren m¨¢s teor¨ªa de categor¨ªas. La demostraci¨®n del ¨²ltimo teorema de Fermat, por ejemplo, se basa en una gran cantidad de matem¨¢ticas del s. XX y la teor¨ªa de categor¨ªas jug¨® all¨ª tambi¨¦n su papel.

Desafortunadamente, este alto nivel de abstracci¨®n super¨® incluso el grado de tolerancia de los propios matem¨¢ticos y, durante a?os, muchos de ellos han considerado esta teor¨ªa como un ¡°sinsentido abstracto¡± y se han limitado a usarla cuando era totalmente necesario para su trabajo. Sin embargo, otros s¨ª aceptaron con los brazos abiertos la belleza y el poder de esta disciplina, lo que hizo que su influencia fuese extendi¨¦ndose de forma gradual no solo en las matem¨¢ticas, sino tambi¨¦n en otras ciencias. A partir de la d¨¦cada de 1990 comenz¨® a infiltrarse en las ciencias de la computaci¨®n: nuevos lenguajes de programaci¨®n como Haskell y Scla, por ejemplo, empleaban ideas de la teor¨ªa de categor¨ªas. Actualmente aparecen nuevas aplicaciones de esta teor¨ªa a la qu¨ªmica, la ingenier¨ªa el¨¦ctrica o ?incluso para dise?ar frenos de los coches! La teor¨ªa de categor¨ªas aplicada, que en otra ¨¦poca hubiese sido considerada un ox¨ªmoron, se est¨¢ convirtiendo en un tema de investigaci¨®n real.

Una categor¨ªa est¨¢ formada por una clase de objetos junto a una clase de morfismos ¨Cun tipo de procesos, o caminos¨C sobre esos objetos

Para entender de qu¨¦ manera se aplica esta teor¨ªa a tantos contextos, es necesario conocer sus ideas b¨¢sicas. Una categor¨ªa est¨¢ formada por una clase de objetos junto a una clase de morfismos ¨Cun tipo de procesos, o caminos¨C sobre esos objetos. Por ejemplo, podemos tomar como objetos las ciudades, y como morfismos las rutas para ir de una ciudad a otra. El requerimiento fundamental que han de cumplir las categor¨ªas es que si tenemos un morfismo de un objeto x a otro y, y otro de y a z, es posible componerlos y obtener un morfismo de x a z. En el ejemplo anterior, si hay una carretera de Madrid a Sevilla, y otra de Sevilla a Faro, entonces esa ruta (Madrid-Sevilla-Faro) conduce de Madrid a Faro. Por tanto, existe una categor¨ªa de las ciudades y las rutas entre ellas.

Aunque el concepto de categor¨ªa es muy simple, explotarlo no lo es tanto. Centrar la atenci¨®n en los morfismos supuso un cambio radical en la perspectiva de las matem¨¢ticas. Desde comienzos de 1900, los l¨®gicos hab¨ªan intentado refundar las matem¨¢ticas sobre principios s¨®lidos, lo que result¨® ser una tarea dif¨ªcil y elusiva. Su mejor baza empleaba la llamada Teor¨ªa de Conjuntos. Un conjunto es, simplemente, una colecci¨®n de elementos. Estos elementos, en la teor¨ªa de conjuntos m¨¢s utilizada por los matem¨¢ticos, son de nuevo, conjuntos. En esa est¨¢tica cosmovisi¨®n, todo es un conjunto. Por su parte, la teor¨ªa de categor¨ªas se construy¨® sobre la teor¨ªa de conjuntos, usando la noci¨®n m¨¢s general de clases, y enfatizando en las maneras de transformar las cosas ¨Clos morfismos¨C, tanto como en las propias cosas. No era incompatible con la teor¨ªa de conjuntos, pero ofrec¨ªa una nueva manera de pensar.

un programa es tambi¨¦n una manera de transformar una serie de datos de entrada en datos de salida y la manera m¨¢s sencilla de construir programas complicados es componer programas m¨¢s simples

Poco a poco, un grupo disperso pero cada vez m¨¢s amplio de investigadores se han ido acercando a esta forma de razonar, aplicando la teor¨ªa de categor¨ªas a temas fuera del ¨¢mbito de las matem¨¢ticas. Por ejemplo, a la programaci¨®n: un programa es tambi¨¦n una manera de transformar una serie de datos de entrada en datos de salida y la manera m¨¢s sencilla de construir programas complicados es componer programas m¨¢s simples.

?ltimamente tambi¨¦n est¨¢n surgiendo novedosas aplicaciones a la ingenier¨ªa y a las ciencias naturales. Por ejemplo, dos de mis estudiantes realizaron pr¨¢cticas en la empresa de ingenier¨ªa Siemens, aplicando teor¨ªa de categor¨ªas a procesos industriales. El primero de ellos, Blake Pollard, ahora ocupa un puesto postdoctoral en el Instituto Nacional de Est¨¢ndares y Tecnolog¨ªa de EE UU. All¨ª, entre otras cosas, ha empleado un m¨¦todo de programaci¨®n basado en teor¨ªa de categor¨ªas para construir una red de energ¨ªa el¨¦ctrica lo suficientemente flexible para manejar los cambios de corriente generados por cientos de casas equipadas por paneles solares.

Hay rumores de que incluso podremos ver, en breve, un instituto de teor¨ªa de categor¨ªas aplicada, que conectar¨¢ a los matem¨¢ticos con programadores o empresarios que requieran esta forma de pensar. Es demasiado pronto para garantizar que estamos al comienzo de una nueva tendencia, pero, desde luego, mis amigos y colegas de Twitter est¨¢n muy emocionados.

John Baez es catedr¨¢tico en el Departamento de Matem¨¢ticas en la Universidad de California Riverside (EE UU) e investigador en el Centro de Tecnolog¨ªas Cu¨¢nticas (Singapur).

Traducci¨®n: ?gata A. Tim¨®n G-Longoria

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter