?Es posible ser 1/3 espa?ol?

Cuando iba al instituto, un profesor de matem¨¢ticas nos propuso una pregunta aparentemente inofensiva: "?es posible ser un 1/3 espa?ol?". Est¨¢ claro que cuando solo uno de los progenitores es espa?ol, su descendencia tiene 1/2 de origen espa?ol. Si solo uno de sus cuatro abuelos es espa?ol, el nieto tiene 1/4 de herencia espa?ola. ?Pero es posible ser exactamente 1/3 espa?ol? A?os despu¨¦s, me encontr¨¦ con la misma pregunta formulada como un problema hidrodin¨¢mico denominado "problema del divisor simple". El famoso matem¨¢tico?Vladimir Arnold (Odesa 1937, Par¨ªs 2010), mi director de tesis en aquel entonces, lo estudi¨® en uno de sus libros.

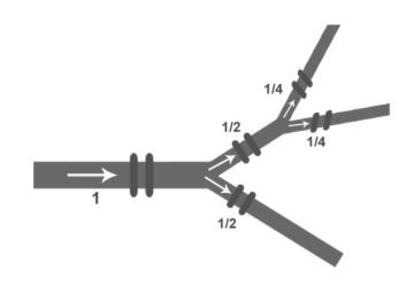
Arnold analiz¨® el problema desde el punto de vista de la din¨¢mica de fluidos: tenemos un r¨ªo con un flujo constante de agua igual a 1 m? de agua por segundo, y un dispositivo llamado divisor simple que permite dividir el cauce en dos corrientes iguales. Aplicando el divisor bifurcamos el r¨ªo en dos riachuelos m¨¢s peque?os con flujos de 1/2 cada uno; si uso otro divisor simple en cada uno de ellos, obtengo corrientes de 1/4 del flujo inicial. La pregunta es: ?se puede usar un n¨²mero finito de divisores simples para conseguir separar un arroyo cuyo flujo sea 1/3 del inicial?

Este problema, seg¨²n contaba Arnold, surgi¨® en los simulacros de defensa civil en el metro de Mosc¨², ya que quer¨ªan dirigir a la multitud hacia tres refugios nucleares iguales. Para ello, necesitaban dividir el flujo de gente mediante torniquetes, que enviaban a una persona a la derecha y la siguiente a la izquierda (bifurcando la cola en dos grupos iguales). Como con el flujo del r¨ªo, buscaban separar el grupo inicial en tres iguales, pasando por sucesivos torniquetes.

Otra manera de formular la cuesti¨®n es la siguiente: tres ladrones quieren dividir su bot¨ªn, sorteando cada objeto mediante una loter¨ªa que ofrezca a cada uno la misma probabilidad de ganar (1/3), pero solo tienen una moneda, as¨ª que quieren hacerlo jugando a cara y cruz. ?Pueden crear un sorteo justo con este m¨¦todo? ?Ves la analog¨ªa entre este problema y el de dividir el r¨ªo en tres cauces iguales?

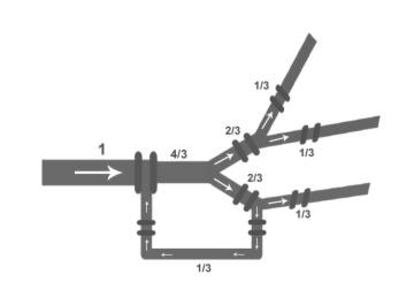
Para resolverlo, algunas personas sugirieron una soluci¨®n asint¨®tica, es decir, dividir el flujo infinitas veces de manera que el flujo de alguno de los riachuelos converge a 1/3. Pero ni para el caso de los ladrones, ni las personas del metro, ni el r¨ªo, ni para las familias, nos valen infinitas divisiones. Hay otra respuesta mucho m¨¢s simple. Se divide el r¨ªo en cuatro cauces iguales (aplicando una vez el divisor, y en cada uno de los dos obtenidos, usando otro m¨¢s), y uno de ellos se reconduce de nuevo a la corriente principal. Los tres restantes son complemente iguales, y cada uno tiene un flujo igual a un tercio del original. Para conseguir cualquier fracci¨®n del flujo se puede usar esta misma idea, simplemente dividiendo en m¨¢s riachuelos, y retornando al cauce inicial los que sean necesarios

Para los tres ladrones, esta soluci¨®n significar¨ªa seguir el siguiente m¨¦todo para rifar cada elemento de su bot¨ªn: en primer lugar, se lanza la moneda dos veces; si se obtienen dos caras, el primer ladr¨®n gana el art¨ªculo; si son primero una cara y luego una cruz, gana el segundo ladr¨®n; si son primero cruz y luego una cara, gana el tercer ladr¨®n; si el resultado son dos cruces, comienza de nuevo el sorteo.

Esta respuesta no sirve para el problema del refugio antia¨¦reo, porque algunas personas quedar¨ªan atrapadas en un bucle y nunca llegar¨ªan a los b¨²nkeres. Y ni siquiera me atrevo a detallar qu¨¦ implicaciones de endogamia y viajes en el tiempo tendr¨ªa este m¨¦todo para obtener un origen de 1/3 espa?ol. Prefiero daros una respuesta con truco: ?S¨ª, uno puede ser 1/3 espa?ol, si sus dos progenitores son 1/3 espa?oles!

Boris Khesin es catedr¨¢tico de Matem¨¢ticas en la Universidad de Toronto (Canad¨¢)

Traducci¨®n: ?gata A. Tim¨®n

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter