Campana sobre campana (matem¨¢tica)

Recorrer la historia de las matem¨¢ticas lleva a lugares inesperados, en este caso a los campanarios de la Inglaterra del siglo XVII. En aquella ¨¦poca, grupos de campaneros ingleses se reun¨ªan regularmente para practicar el arte de ta?er campanas. Se propusieron tocar las campanas de un campanario en todos los ¨®rdenes posibles sin repetici¨®n. Era tal el inter¨¦s que se escribieron varios tratados al respecto, entre ellos ¡°Tintinnalogia¡±, de Richard Duckworth y Fabian Stedman. Este problema anticip¨® una rama de las matem¨¢ticas llamada teor¨ªa de grupos.

El n¨²mero de maneras posibles en el que podemos ordenar n campanas viene dado por n! (le¨ªdo n factorial) y es igual a n!=n.(n-1).(n- 2) ...3.2.1. As¨ª, en un campanario con seis campanas, existen 6! = 6.5.4.3.2.1 = 720 maneras distintas de ta?erlas; pero no basta con enumerar estos posibles ¨®rdenes y tocar uno despu¨¦s de otro, sino que hay que atender a ciertas reglas.

En primer lugar, los campaneros no pueden llevar ¡®partituras¡¯ describiendo la secuencia de ¨®rdenes. Por tanto, hay que buscar un patr¨®n f¨¢cil de recordar, algo que en s¨ª mismo no es demasiado complicado. El problema aparece por las restricciones asociadas a la propia naturaleza de las campanas. Estas son pesadas, van montadas sobre ruedas, y su cadencia es dif¨ªcil de modificar. En la pr¨¢ctica, esto implica que entre una configuraci¨®n y la siguiente solo se puede cambiar el orden de las campanas que han tocado seguidas. Por ejemplo, si tenemos cuatro campanas y las llamamos A, B, C, D, la secuencia ACDB indica que tocamos primero la A, despu¨¦s la C, despu¨¦s la D y finalmente la B. As¨ª despu¨¦s de ACDB podemos ta?er CADB o ACBD o incluso CABD. Sin embargo, despu¨¦s de ACDB no podemos hacer sonar DCAB. Adem¨¢s, por cuestiones est¨¦ticas, se debe empezar y acabar con la misma configuraci¨®n. As¨ª si se empieza con ABCD, se deben recorrer todas las configuraciones respetando la norma anterior y sin repeticiones, para acabar de nuevo en ABCD.

Es posible, y no muy complicado, encontrar un patr¨®n que cumpla las reglas anteriores de forma recursiva. Es decir, conociendo un patr¨®n para un cierto n¨²mero de campanas, se puede dise?ar un patr¨®n para tocar una campana m¨¢s. Se han propuesto varias soluciones de este estilo a lo largo de la historia. Por ejemplo, el inform¨¢tico Donald Knuth, en su c¨¦lebre Art of Computing, cita un algoritmo de Peter Mundy de 1653 que permite hacerlo.

La ¨²ltima condici¨®n sobre los patrones tiene que ver con la sonoridad. La moda del siglo XVII impon¨ªa que una campana no pod¨ªa tocarse en la misma posici¨®n tres veces seguidas. ?Ahora s¨ª tenemos un reto! Stedman encontr¨® una soluci¨®n para este problema con cinco campanas, que est¨¢ recogida en su ¡°Tintinnalogia¡±. Su patr¨®n, conocido como Stedman¡¯s doubles, est¨¢ ¨ªntimamente relacionado con la forma en la que el grupo de isometr¨ªas del pent¨¢gono regular aparece como subgrupo del grupo de permutaciones de las campanas. Si no entiendes de lo que estamos hablando, no te preocupes, Stedman tampoco lo entender¨ªa. Estos son conceptos de una rama de las matem¨¢ticas que no se formaliz¨® hasta dos siglos despu¨¦s, la Teor¨ªa de Grupos.

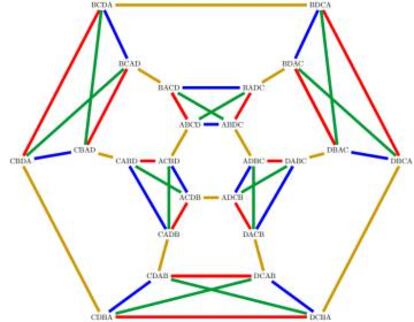
El arte de ta?er campanas mantiene sus adeptos en Inglaterra. En 1963, ocho campaneros ingleses tocaron en la Loughborough Bell Foundry ocho campanas en todos los ¨®rdenes posibles y sin repetici¨®n (un total de 40320 configuraciones distintas). Para ello emplearon 17 horas y 58 minutos. La b¨²squeda de distintos patrones musicales tambi¨¦n contin¨²a. Actualmente se plantea desde una perspectiva que conecta la teor¨ªa de grupos y la teor¨ªa de grafos. Concretamente, la secuencia en la que se tocan los distintos ¨®rdenes de las campanas se corresponde con un camino en un cierto grafo (el grafo de Cayley asociado al grupo de permutaciones) y las restricciones que se imponen al patr¨®n equivalen a propiedades del camino buscado. Este enfoque ya apareci¨® en un trabajo de Robert A. Rankin de 1948, en el que resolv¨ªa un problema sobre campanas de 1741, y pervive en trabajos actuales como este o este.

Yago Antol¨ªn es Ayudante Doctor en la Universidad Aut¨®noma de Madrid y miembro del ICMAT.

Carolina Vallejo es investigadora Juan de la Cierva en la Universidad Aut¨®noma de Madrid y miembro del ICMAT.

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter