Un solo sitio de cruce

Ya hay soluci¨®n para el trig¨¦simo s¨¦ptimo desaf¨ªo matem¨¢tico con el que EL PA?S celebra el centenario de la Real Sociedad Matem¨¢tica Espa?ola., el segundo de los propuestos por los lectores. Francisco Antonio Gonz¨¢lez, desarrollador inform¨¢tico de Indra en San Fernando de Henares (Madrid), propuso el problema (v¨ªdeo de la izquierda), y lo resuelve ahora (v¨ªdeo de la derecha).

Parece que a los lectores les ha costado algo m¨¢s hacerse con este desaf¨ªo: se han recibido en el plazo marcado 120 respuestas, de las que un 75% eran correctas. El ganador de una biblioteca matem¨¢tica como la que entrega cada semana EL PA?S ha sido en esta ocasi¨®n Javier Rodr¨ªguez, de San Sebasti¨¢n de los Reyes (Madrid).

Recordemos brevemente que el desaf¨ªo trataba sobre un nuevo dise?o urban¨ªstico para el pueblo de Bolci. Esta localidad ten¨ªa una sola calle, con 20 parcelas alineadas y numeradas en las que viv¨ªan 26 familias distribuidas como muestra la figura 1. Para mejorar los equipamientos, se iban a derribar las viviendas para construir una manzana de pisos. El proyecto arquitect¨®nico para la nueva distribuci¨®n deb¨ªa respetar tres condiciones: 1) Cada vivienda nueva debe estar completamente ubicada dentro de alguna de las primitivas parcelas; 2) Las familias que ahora son vecinas deben seguir si¨¦ndolo cuando se trasladen a su nueva vivienda; y 3) Ninguna familia se mantiene en su parcela inicial, todas deben cambiar de n¨²mero de parcela.

A partir de ah¨ª, llam¨¢bamos sitio de cruce de un proyecto a dos parcelas que contuvieran al menos un par de familias vecinas que, en la mudanza, intercambiasen entre s¨ª su n¨²mero de parcela. Y el desaf¨ªo consist¨ªa en obtener la cantidad m¨ªnima y m¨¢xima de sitios de cruce que puede llegar a tener un proyecto v¨¢lido, dando las razones que garantizan que no hay posibilidad de construir proyectos v¨¢lidos con una cantidad de sitios de cruce fuera de ese rango.

La soluci¨®n es que en todo proyecto v¨¢lido siempre hay un sitio de cruce y solo puede haber uno. Por tanto, los valores m¨¢ximo y m¨ªnimo coinciden y valen 1.

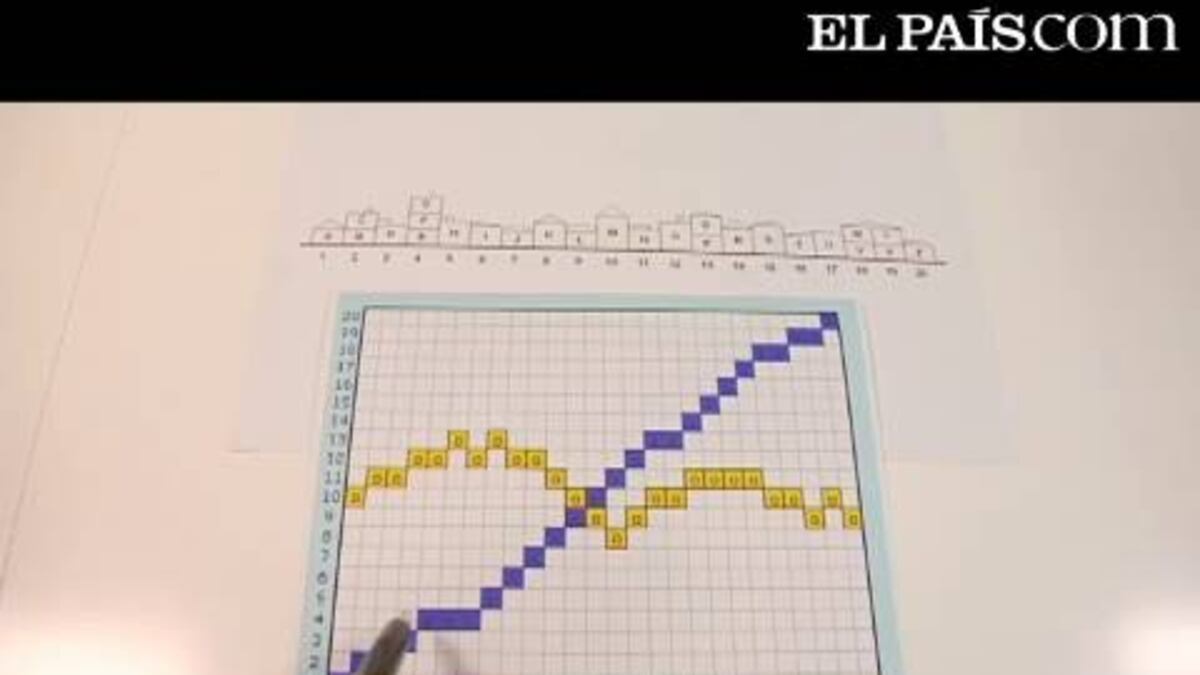
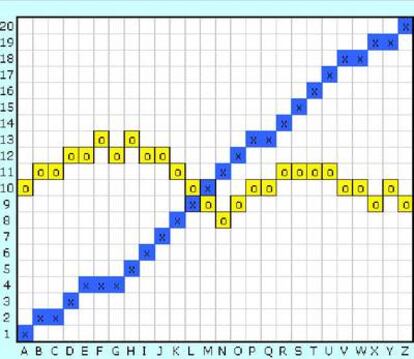
Para demostrarlo, hacemos la gr¨¢fica que se muestra a la izquierda (ver ampliaci¨®n aqu¨ª) con los nombres de las familias en el eje de abscisas y los n¨²meros de parcelas en el eje de ordenadas. A continuaci¨®n, marcamos las celdas que representan una asignaci¨®n familia-parcela. En la gr¨¢fica, hemos representado la situaci¨®n inicial (figura1) con celdas azules y la de nuestro proyecto ejemplo (figura 2) con celdas amarillas. Observemos que la gr¨¢fica azul, relativa a la situaci¨®n inicial, parte de la esquina inferior izquierda y llega a la esquina superior derecha, sin bajar nunca.

Observemos a continuaci¨®n que la gr¨¢fica de un proyecto v¨¢lido, sea cual sea este, deber¨¢ arrancar a la izquierda, necesariamente por encima de la gr¨¢fica azul, y llegar a la esquina derecha, necesariamente por debajo de la gr¨¢fica azul (porque ninguna familia puede repetir parcela y, por tanto, la A deber¨¢ estar por encima de la casilla 1 y la Z por debajo de la 20). Adem¨¢s, ambas gr¨¢ficas deben presentar siempre celdas contiguas (unidas por un lado o por un pico), debido a la necesidad de mantener la relaci¨®n de vecindad y, en los proyectos v¨¢lidos, la gr¨¢fica puede oscilar para arriba y para abajo.

As¨ª, debido a d¨®nde empiezan y terminan, y a que recorren celdas contiguas, las dos gr¨¢ficas tienen necesariamente que cruzarse en alg¨²n momento (deben tener un punto fijo). En nuestro problema, el punto fijo no puede darse en una celda com¨²n, porque eso querr¨ªa decir que hay un vecino que no cambia de parcela. El cruce solo puede ocurrir en un pico de las celdas, tal como sucede en la gr¨¢fica de ejemplo.

Un cruce de este tipo representa a dos familias vecinas que intercambian su n¨²mero de parcela. Dicho de otra forma, el punto fijo de la gr¨¢fica est¨¢ en un sitio de cruce.

Adem¨¢s, al cruzarse las gr¨¢ficas, necesariamente una sube y la otra baja. Puesto que la gr¨¢fica azul nunca baja, esto descarta que pueda haber m¨¢s de un punto fijo, ya que no es posible un cruce que haga pasar la gr¨¢fica amarilla por encima de la azul.

Para completar nuestro razonamiento, debemos asegurarnos ahora de que un sitio de cruce siempre implica la existencia de un punto fijo en la gr¨¢fica. Eso est¨¢ muy claro si en cada parcela solo hay un habitante, porque entonces la representaci¨®n del intercambio de las dos parcelas entre los vecinos es la misma que la del cruce de gr¨¢ficas de nuestro ejemplo. Pueden surgir dudas cuando en la parcela inicial vivan varias familias ya que las familias que intercambian parcela pueden quedar separadas en el eje de la gr¨¢fica.

Pero observemos que, cuando una familia intercambia la parcela con su vecino, si en su parcela inicial hab¨ªa otras familias, entonces todas ellas deben mudarse juntas a la parcela del vecino. Esto ocurre porque cada una de las otras familias debe ir a un lugar que mantenga la vecindad con ambas y, como no se puede quedar en su parcela inicial, acaba necesariamente en la parcela vecina.

Luego, en este caso, las familias se mudan en grupo, y el dibujo de esta situaci¨®n muestra tambi¨¦n necesariamente un cruce de gr¨¢ficas para un par de familias vecinas. En conclusi¨®n: todo sitio de cruce implica la existencia de un punto fijo en la gr¨¢fica, y, por tanto, el punto de cruce tambi¨¦n debe ser ¨²nico.

Otras soluciones

La demostraci¨®n anterior puede hacerse sin utilizar la gr¨¢fica, con un razonamiento que es equivalente al anterior, aunque formulado en otros t¨¦rminos:

Representamos las familias como F(1)=A... F(26)=Z.

Entonces F(n) y F(n+1) representan familias vecinas.

Cada familia, al mudarse, se debe desplazar a la izquierda o a la derecha.

La familia F(1) se desplaza a la derecha y la F(26) a la izquierda.

Debe haber un valor m¨ªnimo de n tal que la familia F(n) se desplace a la izquierda.

La familia anterior a esa, F(n-1), se desplaza a a la derecha.

Se puede ver que entonces que F(n) y F(n-1) tienen que ser dos familias que intercambian de parcela. Con esto hemos demostrado la existencia de un punto de cruce.

Suponiendo la existencia de otro punto de cruce posterior en m, y apoy¨¢ndonos en la observaci¨®n de que es imposible que F(m) se desplace a la izquierda y F(m+1) a la derecha, porque entonces estas familias ser¨ªan vecinas que quedar¨ªan separadas, tambi¨¦n se demuestra que el sitio de cruce es ¨²nico.

Este desaf¨ªo est¨¢ inspirado en el llamado Teorema del punto fijo. Es un teorema matem¨¢tico muy importante y ¨²til. En nuestra soluci¨®n mostramos su versi¨®n m¨¢s sencilla, el caso sobre una dimensi¨®n, pero el teorema tambi¨¦n ofrece variantes muy interesantes para superficies, vol¨²menes y otros casos m¨¢s generales. Varias soluciones mencionan expl¨ªcitamente el Teorema de Bolzano (Alfonso P¨¦rez Arnal sugiere incluso, acertadamente, que esa puede ser la inspiraci¨®n para el nombre del imaginario pueblo de Bolci).

Algunos lectores han cometido un peque?o error de interpretaci¨®n: no han tenido en cuenta que el valor pedido es el de n¨²mero de puntos de cruce, no de familias que intercambian de posici¨®n. As¨ª, tras exponer un argumento correcto, han dado la respuesta de 4 puntos de cruce (es el m¨¢ximo de familias que pueden intercambiar de posici¨®n).

Las respuestas basadas en la gr¨¢fica son algo menos de 1/3 de las correctas, por ejemplo la de Fabio Sarmiento Almeida. Una mayor¨ªa de las respuestas, como la de Eduardo Rodr¨ªguez Golvano, se han basado en argumentos sobre el n¨²mero de parcelas que se han desplazado los vecinos o sobre ir a la derecha o a la izquierda.

Unas pocas versiones de la demostraci¨®n, entre ellas la del ganador del sorteo, plantean demostraciones por recurrencia (a?adiendo parcelas de los extremos) o aumentando el n¨²mero de parcelas de la manzana, y hay una especialmente buena por su concisi¨®n enviada, sin firmar, por RDAVIDA.

Para seguir investigando: Jes¨²s Campos resuelve correctamente el problema y plantea una variante que no termina de resolver: ?cu¨¢l es el n¨²mero m¨¢ximo y m¨ªnimo si no ponemos la restricci¨®n de que las familias que intercambian de parcela sean vecinas?

El jueves plantearemos un nuevo desaf¨ªo.

Un solo sitio de cruce

Un vecindario emprendedor