Una sola medici¨®n

Ya hay soluci¨®n para el trig¨¦simo octavo desaf¨ªo matem¨¢tico con el que EL PA?S celebra el centenario de la Real Sociedad Matem¨¢tica Espa?ola, el tercero y ¨²ltimo de los propuestos por los lectores

Francisco Javier Masip Us¨®n, licenciado en Medicina y jefe de secci¨®n de control de mercado de la D.G. de Consumo del Gobierno de Arag¨®n, lo propuso (ver v¨ªdeo de la izquierda) y ahora lo resuelve (v¨ªdeo de la derecha).

La pr¨¢ctica totalidad de nuestros lectores han demostrado conocer c¨®mo calcular la superficie de un anillo circular. Nos alegra haber conseguido el objetivo de que los desaf¨ªos propuestos por los lectores fuesen variados, tanto en cuanto al tipo de matem¨¢ticas que involucraban como a su dificultad. Se han recibido en el plazo previsto 494 respuestas, de las que un 86% eran correctas; el resto han precisado de un mayor n¨²mero de mediciones. El ganador de una de biblioteca matem¨¢tica como la que entrega cada semana EL PA?S ha sido en esta ocasi¨®n Abel Ib¨¢?ez L¨®pez, de Madrid.

Recordemos brevemente que el desaf¨ªo versaba sobre el c¨¢lculo de una superficie con forma de anillo circular, en una plaza, utilizando para ello el menor n¨²mero de mediciones consideradas entre cada dos puntos.

La soluci¨®n es que basta con una ¨²nica medici¨®n, que se corresponder¨ªa con una cuerda de la circunferencia exterior (el per¨ªmetro de la plaza), que a su vez fuese tangente en un punto a la circunferencia interior (la fuente). Medir¨ªamos la distancia entre los dos puntos en que dicha cuerda corta a la circunferencia exterior; con esa medida, que llamaremos A, es suficiente para calcular la superficie del anillo circular.

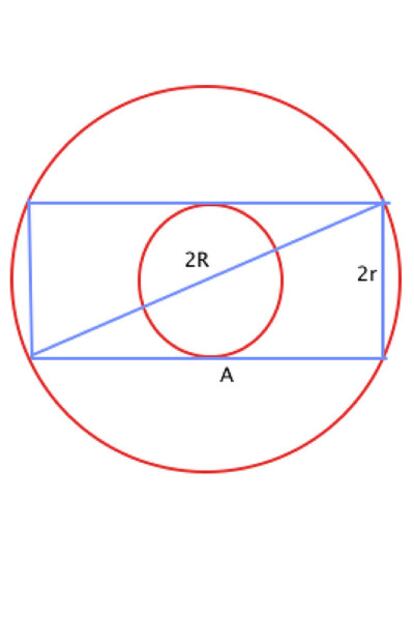
Ya en el plano, dibujaremos, como se muestra en la figura de la izquierda (ver ampliaci¨®n aqu¨ª), la cuerda obtenida (A) y otra paralela a la anterior y tangente en el otro punto de la fuente diametralmente opuesto al precedente. Con esas dos l¨ªneas y las perpendiculares en el punto de corte del c¨ªrculo externo compondremos un rect¨¢ngulo. A continuaci¨®n trazamos la diagonal de ese rect¨¢ngulo y se nos delimitan dos tri¨¢ngulos rect¨¢ngulos en los que un cateto es la cuerda (A), la hipotenusa se corresponde con el di¨¢metro de la circunferencia mayor (2R) y el otro cateto se va a corresponder con el di¨¢metro del c¨ªrculo menor (2r)

Conociendo el cateto A y utilizando el Teorema de Pit¨¢goras tendremos A^2=4R^2 - 4r^2= 4 (R^2 - r^2); de donde (R^2 - r^2) = A^2 /4.

Considerando que el ¨¢rea del anillo ser¨ªa igual a Pi x (R^2 - r^2) y sustituyendo aquel valor en esta f¨®rmula se obtiene que la superficie del anillo es igual a Pi x A^2 /4.

La gran mayor¨ªa de las respuestas correctas han reducido esta soluci¨®n al tri¨¢ngulo que formar¨ªan los radios de ambas circunferencias y la mitad de la cuerda que hemos considerado. Ambas formas de resolver el desaf¨ªo son equivalentes desde un punto de vista matem¨¢tico, ya que se apoyan en tri¨¢ngulos semejantes, y por tanto son igualmente v¨¢lidas. Ahora bien, a la hora de llevarlo a la pr¨¢ctica, tal como nos confirma en su respuesta desde M¨¦xico el ingeniero de caminos c¨¢ntabro Francisco Pi Rodr¨ªguez, la medici¨®n ¨ªntegra de la cuerda ofrecer¨ªa m¨¢s garant¨ªas que la de la simple tangente, que requiere conocer el centro de ambos c¨ªrculos y verificar que se ha trazado correctamente el ¨¢ngulo comprendido entre el radio y la tangente.

La soluci¨®n que se presenta en el v¨ªdeo, incorporando un eje que uniese los dos centros y utilizando la cuerda paralela a ese eje y tangente al c¨ªrculo menor, nos abre el camino para poder calcular la superficie, siempre con una sola medici¨®n, incluso si los c¨ªrculos no fuesen conc¨¦ntricos, como nos comenta tambi¨¦n Luis Alberto G¨®mez Concepci¨®n desde Venezuela.

Una soluci¨®n diferente es la que plantean, de forma muy parecida, Lola M., ?ngel Alonso y Miguel ?ngel Ab¨®s Sanz, utilizando para ello las relaciones trigonom¨¦tricas del ¨¢ngulo que formar¨ªan la cuerda tangente y el radio de la circunferencia mayor que parte desde el punto com¨²n con esa cuerda.

Sergio L¨®pez Goikolea desarrolla un modelo basado en el teorema de la altura, trazando en el plano un di¨¢metro perpendicular a la medici¨®n que se realiza en la plaza, de manera que aquel quedar¨ªa dividido en dos segmentos de longitudes (R + r) y (R - r), cuyo producto se igualar¨ªa al cuadrado de la altura del tri¨¢ngulo que se forma entre ese di¨¢metro y uno de los puntos en los que la cuerda toca a la circunferencia exterior.

Otro tipo de propuestas las plantean Miguel Feror y Jes¨²s Carretero, con matices diferentes, pero ambas basadas en las ecuaciones del c¨ªrculo mayor y la recta tangente; hallando las soluciones o puntos de corte y calculando las distancias entre las mismas.

Son muchas m¨¢s las respuestas que podr¨ªamos destacar por diferentes motivos, entre ellas citaremos las de Enrique Farr¨¦ Rey, quien menciona el Teorema de Holditch y su relaci¨®n con este desaf¨ªo, Jos¨¦ Manuel Ot¨®n, por sus comentarios acerca del problema planteado en la esfera, ?ngel Herrero, por su respuesta narrada en forma de cuento y Violeta Mart¨ªnez Pinilla, de 14 a?os, al parecer la concursante m¨¢s joven entre las respuestas correctas recibidas.

Para finalizar, queremos destacar la respuesta de Iago Vaamonde Paniagua,la m¨¢s original, ingeniosa y bella a todas luces, plasmada en un soneto:

Tengo, Jab¨®n, la cinta en este extremo / tocando la exterior circunferencia. / Avanza t¨² siguiendo con paciencia / el borde mismo con el hilo tenso. // Llegar¨¢s a saber, si es como pienso / como por arte y obra de la ciencia / hilo y fuente hacen una su presencia / con un beso gentil: es el momento. // Dime ya la mitad de la medida, / el¨¦vala al cuadrado en un intento, / multiplica por pi; est¨¢ conseguida. // Calculamos el ¨¢rea del cemento / con un solo medir, austera vida, / no gastaremos m¨¢s, y fin del cuento.

El jueves plantearemos un nuevo desaf¨ªo.

Una sola medici¨®n

Rock and roll en la plaza del pueblo