Matem¨¢ticas e inform¨¢tica: una pareja bien avenida

La serie de televisi¨®n Stark Treck me gustaba mucho de peque?a, sobre todo por el personaje de Spock (Leonard Nimoy). Spock era medio humano, medio vulcano, y sufr¨ªa un conflicto interno entre la raz¨®n y la l¨®gica de su parte vulcana y la emoci¨®n e intuici¨®n de su parte humana. Ahora trabajo en inform¨¢tica, donde a menudo nos enfrentamos a problemas que necesitan de grandes dosis de intuici¨®n y razonamiento l¨®gico para ser resueltos. Recordando a Spock, me pregunto c¨®mo hubiera aplicado ¨¦l la l¨®gica para solucionarlos. Veamos dos ejemplos.

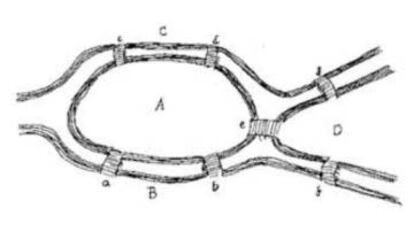
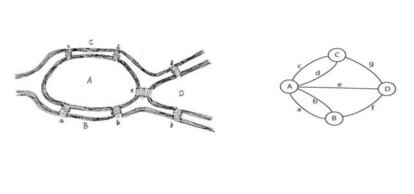
En el siglo XVIII, en la ciudad de K?nigsberg (hoy Kaliningrado), siete puentes conectaban las orillas del r¨ªo Pregel con dos islas (Fig. 1), y se hizo popular el reto de encontrar un camino que recorriera la ciudad, saliendo y llegando al mismo sitio, atravesando una sola vez cada puente.

No sabemos cu¨¢nto tiempo se entretuvieron los vecinos buscando una soluci¨®n, pero s¨ª sabemos, gracias al matem¨¢tico suizo Leonhard Euler, que tal circuito no existe.

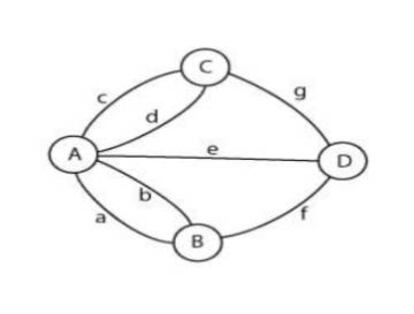
Euler resolvi¨® el problema de manera general en 1736, model¨¢ndolo mediante un grafo, y sus razonamientos dieron origen a la actual teor¨ªa de grafos. El grafo de K?nigsberg (Fig. 2) ten¨ªa cuatro v¨¦rtices ¨CA, B, C, D¨C representando las dos orillas y las dos islas, y siete aristas ¨Ca, b, c, d, e, f, g¨C para representar los puentes. El grafo facilitaba la exploraci¨®n de todos los posibles caminos para comprobar si alguno cumpl¨ªa la condici¨®n. Euler generaliz¨® el problema y comprendi¨® que el tiempo necesario para el an¨¢lisis exhaustivo de todos los caminos de un grafo ser¨ªa enorme al crecer el n¨²mero de v¨¦rtices y aristas. Simplificando un poco, si al llegar a un v¨¦rtice podemos elegir entre dos caminos de salida y el grafo tiene n v¨¦rtices, tendr¨ªamos 2ⁿ posibles caminos. La funci¨®n exponencial crece muy r¨¢pidamente; en nuestra simplificaci¨®n, para los cuatro v¨¦rtices del grafo de K?nigsberg habr¨ªa que comprobar 16 caminos (en realidad, son muchos m¨¢s), pero si el grafo tuviera, por ejemplo, 100 nodos, el ordenador m¨¢s potente del mundo necesitar¨ªa un tiempo muy superior a la edad del universo para analizar las 2¹⁰⁰ rutas.

La genialidad de Euler fue evitar la b¨²squeda exhaustiva. Su mente l¨®gica (hasta donde sabemos genuinamente humana y no vulcana) dedujo que, dado que al llegar a un v¨¦rtice por una arista hay que continuar el circuito saliendo por otra (en total, dos aristas), para que exista una soluci¨®n al problema, el grado de cada v¨¦rtice ¨Cel n¨²mero de aristas que tocan el v¨¦rtice¨C deb¨ªa ser par! Una soluci¨®n simple y elegante a un problema complejo. Desde entonces, en honor a Euler, los caminos que comienzan y terminan en el mismo v¨¦rtice y pasan una sola vez por cada arista se denominan circuitos Eulerianos. Si comienzan y terminan en v¨¦rtices distintos, se denominan caminos Eulerianos.

Teorema de Euler: Un grafo contiene un circuito Euleriano si y solo si cada v¨¦rtice tiene grado par.

Un grafo contiene un camino Euleriano si y solo si dos v¨¦rtices tienen grado impar y el resto grado par.

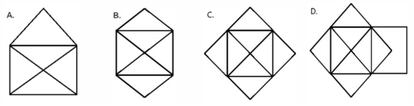
Cuando intentamos dibujar las figuras A, B, C y D de la Fig. 3 sin levantar el l¨¢piz del papel y sin pasar dos veces por la misma l¨ªnea, estamos resolviendo el problema de encontrar un camino Euleriano. Gracias al teorema de Euler, sabemos a simple vista que es posible en el caso de las figuras A, B, y D, pero que es imposible para la figura C.

El segundo problema apareci¨® en el siglo XIX. El astr¨®nomo irland¨¦s Sir William Rowan Hamilton ide¨® un juego denominado el juego icosiano. Propon¨ªa viajar a veinte ciudades, representadas por los v¨¦rtices de un dodecaedro, siguiendo las aristas del mismo pero sin visitar la misma ciudad/v¨¦rtice dos veces. El dodecaedro, de madera, ten¨ªa un clavito en cada v¨¦rtice, donde se pod¨ªa enrollar un cordel para representar el recorrido. El juego no tuvo ¨¦xito.

El problema es parecido al de los puentes. En lugar de buscar un circuito Euleriano (recorrer una sola vez cada arista), hay que buscar un circuito que pase una sola vez por cada v¨¦rtice. Desde entonces, a este tipo de circuitos se les conoce como Hamiltonianos.

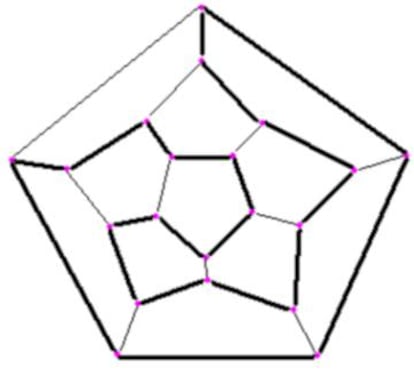
El juego sobre un dodecaedro tiene soluci¨®n (Fig. 4), pero el problema general de decidir si un grafo contiene o no un circuito Hamiltoniano resulta ser extremadamente dif¨ªcil: es un problema NP completo (v¨¦ase el art¨ªculo de Ricardo Pe?a ¡°El problema que los inform¨¢ticos no han podido resolver en 45 a?os¡±). Fig. 4

Conocemos muchas familias de grafos para los que es muy sencillo decidir si existen circuitos Hamiltonianos; pero no tenemos un m¨¦todo general, como el de Euler, v¨¢lido para cualquier grafo. En los casos dif¨ªciles, la ¨²nica opci¨®n es hacer una b¨²squeda exhaustiva, usando un ordenador para evaluar todos los caminos posibles. Muchas personas que trabajamos en inform¨¢tica intentamos encontrar un m¨¦todo m¨¢s inteligente para resolver este problema, o bien demostrar que tal m¨¦todo no existe. Si encontr¨¢semos un m¨¦todo r¨¢pido, adem¨¢s de solucionar el asunto demostrar¨ªamos que P=NP, un dilema que nos trae de cabeza desde 1971. Si demostr¨¢semos que no existe un m¨¦todo mejor que la b¨²squeda exhaustiva, entonces obtendr¨ªamos que P¡ÙNP. La cuesti¨®n ?P=NP? est¨¢ considerada uno de los siete problemas del milenio.

?Por qu¨¦ es tan dif¨ªcil el problema del circuito Hamiltoniano? Se trata de pasar una sola vez por cada v¨¦rtice, mientras que en el caso Euleriano se trata de pasar una sola vez por cada arista. ?Por qu¨¦ este ¨²ltimo resulta en cambio tan sencillo? ?D¨®nde est¨¢ la diferencia?

Como dir¨ªa Spock, ¡°fascinante¡± ?No os parece?

Montserrat Hermo es profesora Titular de la Universidad del Pa¨ªs Vasco

Cr¨®nicas del Intangible es un espacio de divulgaci¨®n sobre las ciencias de la computaci¨®n, coordinado por la sociedad acad¨¦mica SISTEDES (Sociedad de Ingenier¨ªa de Software y de Tecnolog¨ªas de Desarrollo de Software). El intangible es la parte no material de los sistemas inform¨¢ticos (es decir, elsoftware), y aqu¨ª se relatan su historia y su devenir. Los autores son profesores de las universidades espa?olas, coordinados por Ricardo Pe?a Mar¨ª (catedr¨¢tico de la Universidad Complutense de Madrid) y Macario Polo Usaola (profesor titular de la Universidad de Castilla-La Mancha).