Desaf¨ªo criptogr¨¢fico: el c¨®digo secreto del Cofre de los Deseos

Siglos atr¨¢s, la Tierra Tercia estaba dividida en cinco reinos, Reino 1, Reino 2, Reino 3, Reino 4 y Reino 5. Las fronteras entre sus territorios se cruzaban en el Pico C¨²bico, dentro del Bosque M¨¢gico, cuidado por el Mago del Bosque. Tras muchos a?os de guerras constantes entre los reinos, sigui¨® al fin un largo periodo de paz, en el que Mago del Bosque cre¨® una p¨®cima m¨¢gica que conced¨ªa al que la probase cualquier deseo. Para salvaguardar tan peligroso poder, introdujo la p¨®cima dentro de un cofre, que cerr¨® con un candado num¨¦rico que s¨®lo se abr¨ªa introduciendo un n¨²mero secreto. Despu¨¦s, convoc¨® a los l¨ªderes de los cinco reinos, y les habl¨® as¨ª:

¡°Dentro de este cofre he depositado una p¨®cima que conceder¨¢ un deseo a quien beba de ella. Para abrir el cofre es necesario conocer un n¨²mero secreto, del que ahora os dar¨¦ un fragmento a cada uno. Cada vez que alguien beba, vendr¨¦ para cambiar el n¨²mero secreto y repartiros nuevos fragmentos.

Es mi deseo que colabor¨¦is; pues es necesario combinar al menos dos fragmentos para encontrar el n¨²mero secreto:

Mira, amigo, tenemos al frente un cruce de caminos

Uno vertical, de arriba a abajo

Otro horizontal, de izquierda a derecha

Su cruce es un doble cero.

Partamos desde tu punto hasta el m¨ªo,

encontr¨¦monos en el camino vertical,

y pensemos cu¨¢n lejos est¨¢ el cruce; dicha distancia este cofre abrir¨¢

Y as¨ª entreg¨® a cada reino un fragmento, que no era sino una pareja de n¨²meros: al Reino 1 le correspondi¨® el fragmento (1,4), al Reino 2 el (2,1), al Reino 3 el (3,-2), al Reino 4 el (4,-5) y al Reino 5 el (5,-8).

En varios meses no se abri¨® el Cofre de los Deseos. Durante este tiempo, m¨¢s de un l¨ªder, arrastrado por el ansia de un deseo determinado, intent¨® taimadamente obtener por s¨ª solo el secreto a partir de su fragmento¡­ pero sin ¨¦xito. Lleg¨® sin embargo el d¨ªa aciago en el que coincidieron en el Reino 2 y el Reino 5, dos malvados l¨ªderes. Ambos enviaron al Pico C¨²bico a sendos expertos en matem¨¢ticas, que encontraron r¨¢pidamente la manera de calcular el n¨²mero secreto: los fragmentos eran puntos del plano XY, que, por supuesto, defin¨ªan una ¨²nica recta. En el caso de los dos reinos all¨ª presentes, los fragmentos (2,1) y (5,-8) determinaban la recta y = -3x + 7. Esa recta ¡°secreta¡± cortaba el eje de ordenadas (el camino vertical, el eje OY, en el que las x valen 0) en el punto (0,7). Por tanto, razonaron, el n¨²mero secreto que abrir¨ªa el cofre era el 7, pues 7 era la distancia del punto de la recta secreta con el origen, que no era otro que el punto (0,0).

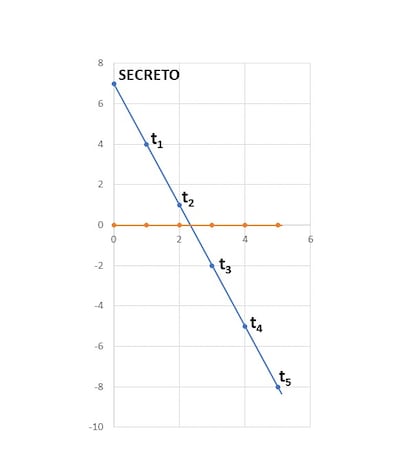
En efecto, probaron con el n¨²mero 7 y el candado se abri¨®. El l¨ªder del Reino 2 bebi¨® un trago de la poci¨®n y pidi¨® quedarse con la cosecha del Reino 3.

Apareci¨® entonces el Mago del Bosque para cerrar el cofre con la p¨®cima en su interior y cambiar el n¨²mero secreto del candado. Tras ello, entreg¨® a los l¨ªderes los nuevos fragmentos: al Reino 1 el fragmento (1,15), al Reino 2 el (2,17), al Reino 3 el (3,19), al Reino 4 el (4,21) y al Reino 5 el (5,23).

Los l¨ªderes de los Reinos 1, 3 y 4 se movieron r¨¢pidamente y acordaron hacer uso del Cofre de los Deseos antes de que lo volviesen a hacer los malintencionados Reinos 2 y 5. Juntando los fragmentos del Reino 1 y el Reino 3, encontraron el n¨²mero secreto y pidieron que el cofre nunca m¨¢s pudiera abrirse de nuevo por una coalici¨®n de los Reinos 2 y 5.

Apareci¨® al instante el Mago del Bosque, convoc¨® a los l¨ªderes de los cinco reinos y les habl¨® as¨ª: ¡°A partir de hoy necesitar¨¦is combinar al menos tres fragmentos para encontrar el n¨²mero secreto y poder as¨ª abrir el Cofre de los Deseos¡±.

Y entreg¨® al Reino 1 el fragmento (1,22), al Reino 2 el (2,29), al Reino 3 el (3,32), al Reino 4 el (4,31) y al Reino 5 el (5,26).

Pasado el tiempo, los Reinos 2 y 5 derrocaron a sus malvados gobernantes. Los l¨ªderes de los Reinos 1, 3 y 4, pensando en establecer una alianza global, decidieron subir una vez m¨¢s al Pico C¨²bico y pedir al Cofre de los Deseos que en adelante, hiciese falta combinar los cinco fragmentos de los cinco reinos para abrir el cofre.

?Cu¨¢l fue el n¨²mero secreto usado por los reinos 1 y 3 para abrir el cofre y pedir que los malvados l¨ªderes de los reinos 2 y 5 no pudieran hacerlo m¨¢s? ?Qu¨¦ n¨²mero secreto usar¨ªan los tres reinos cooperantes en la ¨²ltima ocasi¨®n para abrir el Cofre de los Deseos? ?C¨®mo se las arreglar¨¢ ahora el Mago del Bosque para que sean necesarios cinco fragmentos para abrir el cofre?

Los desaf¨ªos criptogr¨¢ficos se publicar¨¢n cada 15 d¨ªas (aunque en esta ¨²ltima entrega nos hemos retrasado, pedimos disculpas ;-) ). Los lectores pueden dejar sus soluciones y debatir sobre el problema en los comentarios de esta p¨¢gina, por lo que se recomienda a quien quiera resolverlo por s¨ª mismo no leerlos hasta haber descifrado el enigma. Tambi¨¦n pueden enviar sus respuestas al correo desafioscriptograficos@gmail.com. En cada nuevo desaf¨ªo publicaremos la soluci¨®n del anterior, acompa?ada de un comentario con algunas ideas originales o inspiradoras que hayamos recibido.

Javier Herranz es investigador del grupo MAK y profesor de Matem¨¢ticas Aplicadas en la Universitat Polit¨¨cnica de Catalunya.

SOLUCI?N AL DESAF?O ANTERIOR

El anterior desaf¨ªo trataba sobre la criptograf¨ªa visual, un ¨¢rea iniciada por el israel¨ª Adi Shamir (la S del criptosistema RSA) en 1994.

La respuesta a la primera pregunta ¨Dqu¨¦ mensaje se obtiene al superponer la primera transparencia con la segunda que se ha propuesto¨D es que en vez de una A en blanco con fondo negro, se obtiene una L negra en fondo blanco. En realidad a partir de una transparencia dada se podr¨ªa obtener cualquier imagen (que tenga la misma calidad de definici¨®n) utilizando una segunda transparencia apropiada.

En el segundo ejercicio, la imagen recuperada si se juntan las transparencias 1 y 4 o 2 y 3 es:

Nuestros lectores, como (los ya habituales) Joaqu¨ªn y Javier, han llegado a la soluci¨®n sin usar el ¡°mecanismo anal¨®gico¡± sugerido en el texto, utilizando diferente c¨®digo para combinar y luego depurar las im¨¢genes.

Por otro lado, algo similar a lo planteado con im¨¢genes en este desaf¨ªo podr¨ªa hacerse con sonido (como nos planteaba Ramiro por correo, y Salva Fuster desde la secci¨®n de comentarios). De hecho, reproducimos aqu¨ª su reto musical, por si a¨²n alguien se anima a resolverlo:

Una palabra ineludible con un peque?o toque musical (en ocasiones disonante) a dos voces:

A: GDBAB - DBDGD - BABDB - DGECB - CECEG - ECBCE - CEGFC - BCFCF - GFCBC - FCFGG - BABGB

B: FEEBA - EEGFG - ABEGE - ECAFE - FFBAF - FBCBF - BFFGF - EBBBB - FGFCB - GFBFC - ABAAA

- ?Qu¨¦ melod¨ªa act¨²a como clave (hay que tener en cuenta que en la clave, las F realmente son F#)?

- ?Cu¨¢l es la palabra oculta?

- ?Cu¨¢l es el sistema que permite cifrar/descifrar el mensaje?

Un m¨¦todo ac¨²stico se describe tambi¨¦n en el art¨ªculo Audio and Optical Cryptography, propuesto por Desmedt et al., en el congreso ASIACRYPT 98. El lector dispone adem¨¢s una demo on-line asociada al esquema descrito en ese art¨ªculo en este enlace: https://crypto.cs.jmu.edu/visualaudiocrypto/AudioCryptography.htm

Bibliograf¨ªa:

-101 computing: https://www.101computing.net/visual-cryptography/

-Douglas R. Stinson: An Explication of Secret Sharing Schemes. Des. Codes Cryptogr. 2(4): 357-390 (1992)

-Paolo D¡¯Arco, Roberto De Prisco: Visual Cryptography - Models, Issues, Applications and New Directions. SECITC 2016: 20-39

-Giuseppe Ateniese, Carlo Blundo, Alfredo De Santis, Douglas R. Stinson: Visual Cryptography for General Access Structures. Inf. Comput. 129(2): 86-106 (1996)

-Moni Naor, Adi Shamir: Visual Cryptography. EUROCRYPT 1994: 1-12

Puedes seguir a EL PA?S TECNOLOG?A en Facebook y Twitter o apuntarte aqu¨ª para recibir nuestra newsletter semanal.