M¨¦todos infinitos para resolver problemas de car¨¢cter finito

El principio del palomar, uno de los principios m¨¢s fundamentales en matem¨¢ticas, afirma lo siguiente: si distribuimos una cantidad infinita de bolas en una colecci¨®n finita de cajas, hay una caja que contiene una infinidad de bolas. Para comprobar esta afirmaci¨®n, solo usamos dos adjetivos: finito es ¡°peque?o¡± e infinito es ¡°grande¡±, as¨ª como una propiedad: un conjunto grande no puede ser uni¨®n finita de conjuntos peque?os. Hay versiones del principio del palomar en el caso finito, que implican heur¨ªsticamente que habr¨¢ varias personas en el mismo barrio de la misma ciudad con la pol¨¦mica cazadora amarilla. Para ser m¨¢s precisos, para que en una ciudad con diez barrios, haya al menos tres personas en el mismo barrio con la misma prenda, basta haber vendido al menos (3-1)*10+1=21 cazadoras. Sin embargo, para dar con este valor hay que pensar m¨¢s que en el caso de la dicotom¨ªa finito-infinito.

La dicotom¨ªa previa finito-infinito permite tratar problemas en muchos ¨¢mbitos de las matem¨¢ticas. Un ejemplo cl¨¢sico, de enunciado elemental y f¨¢cil, pero cuya soluci¨®n dista de serlo, es el siguiente: si pintamos los n¨²meros naturales con dos colores, por ejemplo rojo y verde (sin tendencias pol¨ªticas ocultas), el principio del palomar implica que hay una cantidad infinita de n¨²meros del mismo color. Sin embargo, ?podemos encontrar un conjunto infinito de n¨²meros del mismo color tal que toda suma de los mismos tambi¨¦n tendr¨¢ ese color? Una respuesta afirmativa implica la existencia de un tri¨¢ngulo monocrom¨¢tico de la forma (x, y, x+y), que el matem¨¢tico ruso Issai Schur ya demostr¨® en 1916.

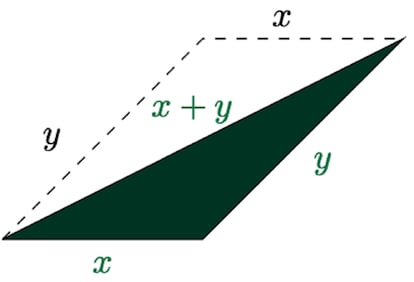
Neil Hindman proporcion¨® en 1974 una respuesta afirmativa al problema anterior en lo que hoy se conoce como el teorema de Hindman. Su demostraci¨®n, aunque usa t¨¦cnicas elementales, es especialmente enrevesada. En el oto?o de 1975 Frederick Galvin y Steven Glazer proporcionaron una nueva demostraci¨®n elegante y sucinta, estableciendo una conexi¨®n inesperada. Recurrieron al uso de un objeto matem¨¢tico llamado ultrafiltro, el cual se apoya precisamente en la dicotom¨ªa peque?o-grande.

Un ultrafiltro es, esencialmente, una clasificaci¨®n de todo subconjunto de los n¨²meros naturales en dos categor¨ªas, ¡°grandes¡± y ¡°peque?os¡±, de tal forma que la uni¨®n de dos subconjuntos ¡°peque?os¡± cualesquiera no sea ¡°grande¡±. Se captura as¨ª la propiedad previa del principio del palomar. Ultrafiltros hay muchos; por ejemplo, obtenemos uno si denotamos un subconjunto como ¡°grande¡± cuando contiene el n¨²mero 42, y ¡°peque?o¡± todo aquel que no lo contenga. Un peque?o inciso para el lector versado: como un ultrafiltro es una medida de probabilidad finitamente aditiva con valores posibles 0 y 1, el ultrafiltro prev¨ªo es una Delta de Dirac concentrada en el punto 42. Con este ultrafiltro muchos conjuntos finitos son ahora ¡°grandes¡±. Encontrar ultrafiltros que solo seleccionen como ¡°grandes¡± conjuntos infinitos es menos obvio y mucho m¨¢s interesante, puesto que su existencia se sigue del esot¨¦rico axioma de elecci¨®n, que tantos recelos causa a ciertos matem¨¢ticos.

En la demostraci¨®n de Galvin y Glazer, demuestran la existencia de un ultrafiltro con la propiedad siguiente: si clasifica un conjunto A como ¡°grande¡±, entonces A contiene un subconjunto infinito B tal que toda suma de n¨²meros en B est¨¢ en A

En la demostraci¨®n de Galvin y Glazer, demuestran la existencia de un ultrafiltro con la propiedad siguiente: si clasifica un conjunto A como ¡°grande¡±, entonces A contiene un subconjunto infinito B tal que toda suma de n¨²meros en B est¨¢ en A. Con ese ultrafiltro, el teorema queda demostrado: o bien los n¨²meros rojos o bien los verdes forman un conjunto ¡°grande¡±, y as¨ª se obtiene el conjunto monocrom¨¢tico con la propiedad de Hindman.

Esta demostraci¨®n del teorema de Hindman es un mero ejemplo del uso de ultrafiltros en matem¨¢ticas. De hecho, los ultrafiltros permiten resolver sin dolores de cabeza una pl¨¦tora de resultados algebraicos, combinatorios y particularmente en teor¨ªa de modelos, gracias al c¨¦lebre teorema del polaco Jerzy ?o? (su apellido se pronuncia como la palabra inglesa wash). El mismo Hindman reconoci¨® p¨²blicamente que no hay mejor castigo que leer su demostraci¨®n original, y aboga desde entonces con fervor por el uso de los ultrafiltros en las matem¨¢ticas. Los autores de esta columna, as¨ª como muchos matem¨¢ticos de gran nivel, comparten la convicci¨®n de Hindman sobre la utilidad de los ultrafiltros como herramienta matem¨¢tica.

El¨ªas Baro Gonz¨¢lez es contratado doctor en la Universidad Complutense de Madrid.

Amador Mart¨ªn Pizarro es profesor en la Universidad Albert-Ludwig de Friburgo (Alemania).

Daniel Palac¨ªn Cruz es ayudante doctor en la Universidad Albert-Ludwig de Friburgo (Alemania).

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: "Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas".

Edici¨®n y coordinaci¨®n: ?gata Tim¨®n (ICMAT).

Puedes seguir a Materia en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter