Las simetr¨ªas de las ecuaciones del universo
La llamada teor¨ªa de reducci¨®n busca simplificar la geometr¨ªa de los sistemas f¨ªsicos haciendo uso de sus simetr¨ªas, de forma que las ecuaciones resultantes sean m¨¢s sencillas de interpretar y resolver

¡°La naturaleza es siempre m¨¢s sutil, m¨¢s compleja y m¨¢s elegante que lo que somos capaces de imaginar¡±, afirmaba el divulgador cient¨ªfico Carl Sagan. Desde hace siglos, la f¨ªsica se ocupa de imaginar y comprender el funcionamiento del universo, para despu¨¦s describirlo empleando ecuaciones matem¨¢ticas. Sin embargo, en muchas ocasiones, las ecuaciones que se plantean son muy dif¨ªciles de resolver o interpretar. Por suerte, hay una interesante caracter¨ªstica de algunos sistemas f¨ªsicos que nos ayuda en esta labor: la simetr¨ªa.
Los sistemas con simetr¨ªa permanecen invariantes al aplicarles cierta transformaci¨®n. Por ejemplo, el cuadrado posee una simetr¨ªa de rotaci¨®n, ya que si lo giramos 90 grados (o sus m¨²ltiplos, 180, 270¡) en torno a su centro, se mantiene igual. No obstante, si elegimos un ¨¢ngulo distinto de los anteriores, el cuadrado resultante no coincide con el inicial. En este caso, cuando solo algunos ¨¢ngulos son v¨¢lidos, decimos que la simetr¨ªa es discreta. En contraposici¨®n, hay otras figuras, como la circunferencia, que quedan invariantes frente a cualquier rotaci¨®n en torno a su centro. Este segundo tipo de simetr¨ªa se denomina continua.

A principios del siglo XX, Emmy Noether (1882-1935), una de las personalidades m¨¢s importantes de la historia de las matem¨¢ticas, descubri¨® que estas simetr¨ªas continuas ayudan a entender las leyes f¨ªsicas y a resolver sus ecuaciones. El famoso teorema de Noether, una de sus muchas contribuciones a las matem¨¢ticas y a la f¨ªsica te¨®rica, afirma que, cuando un sistema f¨ªsico posee una simetr¨ªa continua, aparece una cantidad que se conserva durante la evoluci¨®n del sistema. Esto nos permite simplificar las ecuaciones, pues la funci¨®n matem¨¢tica que representa dicha cantidad es constante.
Un ejemplo importante son los sistemas en los que las leyes f¨ªsicas que los rigen no cambian con el tiempo ¨Ces decir, el resultado de los experimentos no depende del instante en el que los llevemos a cabo, siempre que mantengamos las condiciones en las que tiene lugar¨C. Estos sistemas poseen, por tanto, simetr¨ªa bajo traslaciones temporales, as¨ª que, seg¨²n el teorema de Noether, se conserva una cierta cantidad: la energ¨ªa mec¨¢nica ¨Cla suma de su energ¨ªa cin¨¦tica y su energ¨ªa potencial¨C. Es el caso de la atracci¨®n gravitatoria: al dejar caer un objeto al suelo, la gravedad lo atrae con la misma intensidad hoy, ma?ana o dentro de unos a?os. Aplicando el teorema de Noether, se puede afirmar que la energ¨ªa mec¨¢nica del objeto se mantiene constante durante su ca¨ªda.
Aunque este teorema constituye una herramienta fundamental para entender y simplificar los sistemas que poseen simetr¨ªas, todav¨ªa se puede ir m¨¢s all¨¢. Esto es lo que hicieron durante los a?os 70 del siglo pasado matem¨¢ticos como Kenneth Meyer, Jerrold Marsden o Alan Weinstein en la denominada teor¨ªa de reducci¨®n. La principal idea de esta teor¨ªa es utilizar las simetr¨ªas continuas para simplificar la geometr¨ªa de los sistemas, reduciendo su dimensi¨®n. A su vez, esto conlleva una disminuci¨®n del n¨²mero de variables de las ecuaciones.
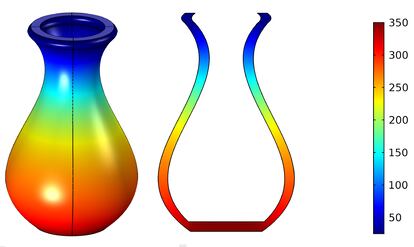
Veamos qu¨¦ significa esto con un ejemplo. Supongamos que queremos describir una vasija de arcilla elaborada con un torno. Debido al movimiento de rotaci¨®n con el que ha sido creada, la vasija tiene simetr¨ªa de revoluci¨®n. En consecuencia, para conocer el dise?o de toda la vasija es suficiente con conocer su perfil. As¨ª, se ha reducido la geometr¨ªa de la vasija (un volumen) a la geometr¨ªa de su perfil (una superficie) gracias a la simetr¨ªa de revoluci¨®n. Es m¨¢s, podemos estudiar cualquier proceso que respete esta simetr¨ªa solamente analizando lo que sucede en el perfil. Por ejemplo, para saber c¨®mo se calienta al ser expuesta a una fuente de calor ¨Cque respete esta simetr¨ªa¨C basta con conocer la evoluci¨®n de la temperatura a lo largo del perfil.
Tanto la teor¨ªa de reducci¨®n, como el teorema de Noether surgieron dentro de la mec¨¢nica geom¨¦trica ¡ªla formalizaci¨®n de la mec¨¢nica cl¨¢sica como una rama de la geometr¨ªa diferencial¡ª, pero posteriormente fueron extendidos a las llamadas teor¨ªas de campos, que constituyen una generalizaci¨®n de las ideas de la mec¨¢nica geom¨¦trica a contextos m¨¢s amplios. Esto hace que sean de utilidad en un gran n¨²mero de problemas f¨ªsicos, desde cuestiones de la mec¨¢nica de fluidos, hasta de la f¨ªsica de part¨ªculas elementales. Por ejemplo, la ecuaci¨®n del movimiento correspondiente a una fuerza de Lorentz ¡ªla fuerza que experimenta una part¨ªcula cargada el¨¦ctricamente sumergida en un campo magn¨¦tico¡ª se obtiene aplicando este proceso de reducci¨®n.
A pesar de estos avances, siguen apareciendo nuevos retos en el estudio de los espacios reducidos y de las ecuaciones correspondientes que la investigaci¨®n actual est¨¢ tratando de resolver, lo que convierte a la teor¨ªa de la reducci¨®n en un campo todav¨ªa en desarrollo y con un gran potencial.
?lvaro Rodr¨ªguez Abella es investigador predoctoral en el Instituto de Ciencias Matem¨¢ticas (ICMAT)
Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.
Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n Garc¨ªa-Longoria (ICMAT)
Puedes seguir a MATERIA en Facebook, Twitter, Instagram o suscribirte aqu¨ª a nuestra newsletter
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
M¨¢s informaci¨®n

Grandes retos en las ecuaciones de los fluidos





























































