Empaquetamiento compacto

El problema del mensaje secreto planteado la semana pasada se resuelve, parad¨®jicamente, complic¨¢ndolo m¨¢s: el caballero a?ade un segundo candado a la caja y se la env¨ªa de vuelta a la dama, que quita el primer candado y vuelve a mand¨¢rsela al caballero, que ahora no tiene m¨¢s que abrir su propio candado. Un sistema lento pero seguro, pues todo el tiempo el mensaje queda fuera del alcance del indiscreto mensajero.

Si cambiamos los candados por grandes n¨²meros primos, tenemos un eficaz sistema de encriptado ampliamente difundido. Imaginemos que, en tiempos preinform¨¢ticos, A quiere compartir con B dos n¨²meros secretos: 1901 y 2713 (o la diferencia entre ambos: 2713 ¨C 1901 = 812). A multiplica ambos n¨²meros y env¨ªa el resultado a B por correo o por tel¨¦fono sin temor, pues, aunque alguien sospechara que 5157413 es el producto de dos n¨²meros significativos, sin ayuda de un ordenador es sumamente dif¨ªcil hallar esos factores (y con ayuda de un ordenador tambi¨¦n, si los primos son lo suficientemente grandes). B, a su vez, multiplica el n¨²mero recibido por otro primo de cuatro cifras, por ejemplo, 1301, y env¨ªa el producto, 6709794313, a A, que lo divide por uno de sus dos primos, por ejemplo, 1901, y le env¨ªa el resultado a B, que al dividirlo por su propio primo obtiene el otro primo de A: 3529613/1301 = 2713.

He utilizado primos de solo cuatro cifras para ilustrar este sistema de encriptado (conocido como RSA por sus creadores: Rivest, Shamir y Adleman), pero en la actualidad, y dada la enorme capacidad de c¨¢lculo alcanzada por los ordenadores, los primos utilizados han de ser de cientos de cifras para garantizar la seguridad.

En relaci¨®n con los dem¨¢s problemas de la semana pasada, ver la secci¨®n de comentarios correspondiente, donde han sido ampliamente analizados.

De las cajas a los paquetes

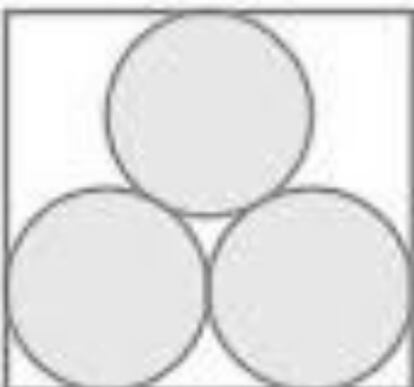
Aunque no todos: el problema 2 no mereci¨® la atenci¨®n de mis sagaces lectoras/es, que se centraron en el mensaje secreto y las bolas viajeras. Y sin embargo es un interesante problema de empaquetamiento que vuelvo a proponer acompa?ado de una vista cenital de la caja (sin tapa):

En una caja orto¨¦drica hay tres bolas de 10 cent¨ªmetros de di¨¢metro tangentes entre s¨ª y tangentes a las paredes, la base y la tapa de la caja. ?Cu¨¢nto miden los lados de la caja?

El apilado y el empaquetamiento de esferas del mismo tama?o es una cuesti¨®n que ha interesado a matem¨¢ticos e ingenieros desde antiguo. El matem¨¢tico y astr¨®nomo brit¨¢nico Thomas Harriot (que, entre otras cosas, introdujo en la notaci¨®n matem¨¢tica los s¨ªmbolos > y <) fue el primero en calcular, a mediados del siglo XVI, el n¨²mero de balas de ca?¨®n que hay en una pila en forma de pir¨¢mide de base cuadrada (?cu¨¢ntas son?), y Gauss demostr¨® que la m¨¢xima densidad obtenible al llenar el espacio tridimensional de esferas iguales es aproximadamente 3/4 (exactamente ¦Ð/3¡Ì2). La densidad de un empaquetamiento es la fracci¨®n de espacio ocupada por las esferas. ?C¨®mo es este empaquetamiento de m¨¢xima densidad?

Bajando de 3 dimensiones a 2, el empaquetamiento de esferas en el espacio se convierte en el empaquetamiento de c¨ªrculos en el plano. Y de nuevo fue Gauss quien demostr¨® que la m¨¢xima densidad se consigue, en este caso, mediante la disposici¨®n hexagonal, en la que cada c¨ªrculo est¨¢ rodeado por otros 6 tangentes a ¨¦l. ?Puedes calcular la densidad de este empaquetamiento? Para evitar el efecto distorsionador de los bordes de una superficie real, el problema se plantea en un plano infinito.

Si los c¨ªrculos as¨ª empaquetados fueran el¨¢sticos y crecieran apret¨¢ndose unos contra otros, formar¨ªan una ret¨ªcula hexagonal. Eso es, de hecho, lo que ocurre en un panal de abejas.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.