Anna Kiesenhofer: del infinito al oro ol¨ªmpico

En 2016 Anna Kiesenhofer defendi¨® su tesis doctoral en la Universidad Polit¨¦cnica de Catalu?a (UPC), en un ¨¢rea de las matem¨¢ticas llamada geometr¨ªa simpl¨¦ctica. En 2021, el pasado 25 de julio, la matem¨¢tica austriaca obtuvo, para la sorpresa de muchos, el oro ol¨ªmpico en la prueba de ciclismo en ruta de los Juegos Ol¨ªmpicos de Tokio. El grupo holand¨¦s, favorito en la competici¨®n, no supo contar las ciclistas que estaban en la escapada y, tras superar a la polaca Anna Plichta y a la israel¨ª Omer Shapira, pensaron que no quedaba nadie m¨¢s por delante; se olvidaron de Kiesenhofer. A pesar de este error, la ventaja y el empe?o de la austriaca en los ¨²ltimos kil¨®metros hubieran hecho muy dif¨ªcil que la alcanzaran.

Tanto en su carrera deportiva como en la matem¨¢tica, Kiesenhofer ha hecho gala de dos atributos fundamentales: disciplina y persistencia. Porque, por mucho que se empe?e Hollywood, en la vida real ni las grandes conjeturas se demuestran por inspiraci¨®n divina, ni las medallas ol¨ªmpicas se ganan por casualidad. Detr¨¢s de una victoria ¨Cdeportiva o cient¨ªfica¨C se esconden tambi¨¦n derrotas y adversidades, que es posible afrontar gracias a la resiliencia.

Anna Kiesenhofer estudi¨® un doble grado de Matem¨¢ticas y F¨ªsica en la Universidad de Viena y obtuvo su m¨¢ster en Matem¨¢ticas en la Universidad de Cambridge. En 2012 lleg¨® al Laboratorio de Geometr¨ªa y Sistemas Din¨¢micos de la UPC para desarrollar su doctorado junto a Eva Miranda ¨Ccoautora de este art¨ªculo¨C sobre un tipo de estructura, llamadas b-variedades simpl¨¦cticas. En 2009, Miranda, junto con Victor Guillemin y Ana Rita Pires, hab¨ªa comenzado el estudio de estos objetos, motivada por el an¨¢lisis de magnitudes m¨¦tricas ¨Ccomo es el ¨¢rea¨C que tienden a infinito.

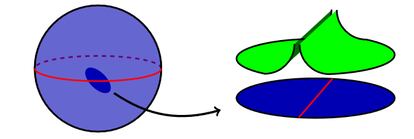
Imaginemos un globo terr¨¢queo fabricado con chicle y cortado por el ecuador en dos partes; el resultado son dos superficies con borde, correspondientes al hemisferio norte y al hemisferio sur. Podemos estirar su borde ilimitadamente y el ¨¢rea de los hemisferios crecer¨¢ de la misma manera. En este caso, podr¨ªamos decir que la esfera ¨Cel objeto del que part¨ªamos¨C admite una estructura de variedad b-simpl¨¦ctica.

Las variedades b-simpl¨¦cticas han resultado muy ¨²tiles para estudiar diversos problemas de la mec¨¢nica celeste, por ejemplo, para analizar colisiones de los cuerpos celestes. Conjuntamente con su directora, Anna Kiesenhofer estudi¨® cierto tipo de sistemas ¨Cintegrables¨C en estas variedades y sus perturbaciones.

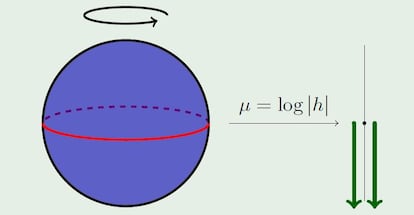
Como casi todas las tesis aquella fue, de cierta manera, un pulso al infinito. Habitualmente, la persona que est¨¢ realizando el doctorado debe resolver a uno o varios problemas en un periodo de tiempo acotado. Con ello se ejercita no solo el m¨²sculo matem¨¢tico, sino tambi¨¦n se aprende sobre la organizaci¨®n del trabajo investigador, identificando, peleando y disfrutando peque?as y grandes metas. Tambi¨¦n es un periodo de aprendizaje introspectivo, en el que hay que hacer frente a las propias limitaciones y a las fortalezas.

Todo ello culmina con la defensa de la tesis, lo que para algunos supone un punto y final y para otros un preludio de la carrera investigadora. En el caso de Kiesenhofer, fue el principio de una trayectoria en la que combinar¨ªa dos de sus pasiones. Ese mismo a?o, en 2016, consigui¨® la victoria en la carrera general de la Copa de Espa?a de ciclismo y salt¨® a la fama internacional en el Tour Cycliste F¨¦minin International de l¡¯Ard¨¨che, cuando coron¨® como ganadora el Mont Ventoux, quiz¨¢s la cumbre m¨¢s m¨ªtica, y qued¨® segunda en la final general.

Despu¨¦s de estos ¨¦xitos recibi¨® varias ofertas de contratos y, en la temporada de 2017, compiti¨® con el equipo del Lotto. Sin embargo, debido a problemas f¨ªsicos que declar¨® estar padeciendo, no fue capaz de rendir como se esperaba, as¨ª que decidi¨® retirarse y volver a las matem¨¢ticas. Ese mismo a?o obtuvo una plaza postdoctoral en la Escuela Polit¨¦cnica Federal de Lausana (Suiza) para incorporarse al grupo de ecuaciones en derivadas parciales. Kiesenhofer y Miranda contin¨²an su colaboraci¨®n, estudiando simetr¨ªas generales en las variedades b-simpl¨¦cticas.

En 2019 volvi¨® a las competiciones ciclistas y gan¨® el Campeonato Austr¨ªaco Contrarreloj en los siguientes tres a?os, as¨ª como el de Ruta en 2019. En 2021, sin ning¨²n patrocinio, ha competido por primera vez en los Juegos Ol¨ªmpicos, en el equipo austriaco. Su victoria, como destacan los medios, ha requerido un derroche de fuerza y una perfecta dosificaci¨®n de su ventaja en el circuito de Fuji. Fue una muestra de sus aptitudes f¨ªsicas y mentales, pero tambi¨¦n de su trabajo de entrenamiento, su excelente preparaci¨®n y su af¨¢n de superaci¨®n. Todas ellas, caracter¨ªsticas que tambi¨¦n definen su carrera matem¨¢tica.

Manuel de Le¨®n es Profesor de Investigaci¨®n del CSIC en el Instituto de Ciencias Matem¨¢ticas (ICMAT) y acad¨¦mico de la Real Academia de Ciencias.

Eva Miranda es catedr¨¢tica ICREA Academia de la Universidad Polit¨¦cnica de Catalu?a, miembro del Centre de Recerca Matem¨¤tica y del Observatoire de Par¨ªs (Francia) e investigadora asociada al ICMAT.

?gata Tim¨®n G-Longoria es coordinadora de la Unidad de Cultura Matem¨¢tica del ICMAT y editora y coordinadora de esta secci¨®n

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.