Estrategia segura

Los juegos de estrategia segura son aquellos en los que uno de los dos jugadores, que puede ser quien hace el primer movimiento o quien hace el segundo, siempre gana si efect¨²a en todo momento las jugadas correctas. Y tambi¨¦n hay juegos de estrategia segura que terminan necesariamente en empate si ambos jugadores hacen siempre la mejor jugada.

Si en el ajedrez hubiera una estrategia ganadora segura para las negras (que son las que hacen el segundo movimiento), posibilidad que se plante¨® la semana pasada, las blancas podr¨ªan hacer una jugada ¡°nula¡± (por ejemplo, sacar un caballo y luego devolverlo a la posici¨®n de partida) para usurpar el papel ¡°segund¨®n¡± de las negras, lo que demuestra que una partida de ajedrez en la que ambos jugadores juegan de la mejor manera posible solo puede terminar en tablas o con la victoria de las blancas, ya que la jugada inicial (apertura) puede ser ventajosa o indiferente, pero no perjudicial. ?Es correcto este razonamiento o tiene alg¨²n punto d¨¦bil?

El alquerque y el molino, como hemos visto en entregas anteriores, son juegos de estrategia segura que terminan en empate si ambos jugadores juegan de la mejor manera posible, y lo mismo ocurre con las damas en el tablero de 8x8 y con doce fichas por bando, derivadas del alquerque. Sin embargo, en el caso de las damas polacas, en un tablero de 10x10 y con veinte fichas por bando, a¨²n no se ha podido demostrar (que yo sepa) que la partida termine necesariamente en empate si se sigue la estrategia ¨®ptima, aunque se considera que eso es lo m¨¢s probable.

El nim y sus variantes

Uno de los juegos de estrategia segura m¨¢s sencillos y populares es el nim, del que hay numerosas variantes. La m¨¢s simple consiste en poner 20 objetos peque?os (monedas, cerillas, guijarros¡­) en fila e ir quitando por turnos entre una y tres unidades; pierde el que se lleva la ¨²ltima pieza. En esta modalidad hay una sencilla estrategia ganadora, ?cu¨¢l es? ?C¨®mo se puede generalizar el resultado a n objetos, de los que se pueden retirar entre 1 y p cada vez?

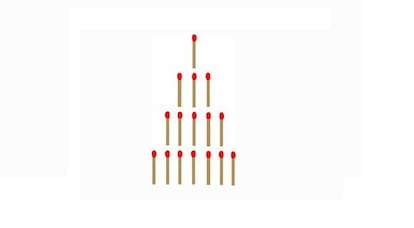
Para complicar un poco la cosa, se pueden disponer los objetos -pongamos que son cerillas- en varias filas de distinto n¨²mero; por ejemplo, en cuatro filas de 1, 3, 5 y 7 cerillas respectivamente. Los dos jugadores, por turnos, retiran de una a tres cerillas, todas de la misma fila, y pierde el que se queda con la ¨²ltima. En este caso la estrategia ganadora no es tan simple, pero existe. ?Cu¨¢l es? ?Qui¨¦n tiene asegurada la victoria si juega correctamente, el primero o el segundo en jugar?

Otra variante consiste en poder llevarse todas las cerillas que se quiera de una misma fila, y el n¨²mero de filas y de cerillas por cada fila se puede variar a voluntad. L¨®gicamente, cuantas m¨¢s filas y cerillas, m¨¢s complicado se vuelve el juego.

Volviendo al tablero de ajedrez (siempre volvemos a ¨¦l), hay una variante del nim que se juega con fichas de damas sobre un tablero de 8x8. Un jugador coloca ocho fichas blancas en la primera fila y el otro ocho fichas negras en la ¨²ltima, como se ve en la figura. Luego, por turno, cada jugador mueve una de sus fichas hacia delante tantas casillas como desee, hasta que la ficha blanca y la negra de una misma columna lleguen a casillas contiguas, en cuyo caso ninguna de las dos puede seguir moviendo. Gana el jugador que hace el ¨²ltimo movimiento. ?Por qu¨¦ es este juego una variante del nim? ?Cu¨¢l de los dos jugadores gana necesariamente si efect¨²a las jugadas correctas y cu¨¢l es su estrategia ganadora?

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal