El alquerque

Al cortar una baraja de 52 cartas, en teor¨ªa podemos separar entre 0 y 51, ya que es posible el corte nulo o no-corte, que se suele indicar dando unos golpecitos con los dedos sobre el mazo (separar las 52 cartas equivale al corte nulo, ya que el mazo se queda como estaba). Y digo ¡°en teor¨ªa¡± porque en la pr¨¢ctica nadie separa, por ejemplo, 1 carta o 51 (ser¨ªa incluso dif¨ªcil f¨ªsicamente), y el corte suele situarse hacia la mitad del mazo, por lo que la probabilidad de formar dos montones iguales, pedida la semana pasada, es sustancialmente mayor que la probabilidad te¨®rica, que es 1/52.

En cuanto a la probabilidad de que un mont¨®n sea el doble que el otro, mis sagaces lectoras/es se habr¨¢n dado cuenta de que es una pregunta trampa/broma: 52 no es divisible por tres, y, por tanto, la probabilidad es 0. Pero si el que reparte es Ace in the Sleeve Morgan, que una de cada dos veces se mete un as en la manga, la probabilidad de que haya solo 51 cartas es 1/2, y en ese caso se puede conseguir que un mont¨®n sea el doble del otro separando 17 o 34 cartas; por lo tanto, la probabilidad pedida, si reparte Morgan, es 1/2 x 2/51 = 1/51 (huelga se?alar que en este caso la probabilidad 0 es la de que haya dos montones iguales).

En cuanto a la probabilidad de que nos toque al menos un as en una mano de p¨®ker, se obtiene m¨¢s f¨¢cilmente calculando la probabilidad contraria, es decir, la de que no nos toque ninguno. Puesto que cuatro de las 52 cartas son ases, la probabilidad de que la primera que nos dan no sea un as es 48/52, la de que tampoco lo sea la segunda es 47/51, la tercera 46/50, la cuarta 45/49 y la quinta 44/48; por lo tanto, la probabilidad de que ninguna sea un as es el producto de estas cinco fracciones: 35673/54145, y la de que salga alguno ser¨¢ la probabilidad complementaria: 1 ¨C 35673/54145 = 18472/54145, aproximadamente 1/3. De modo que si a lo largo de una partida de p¨®ker no te sirven al menos un as un tercio de las veces, puede que est¨¦s jugando con Ace in the Sleeve Morgan.

Del alquerque a las damas

Del Grupo Alquerque de Sevilla, mencionado en las ¨²ltimas semanas, no solo cabe se?alar sus valiosas aportaciones a la did¨¢ctica de las matem¨¢ticas, sino tambi¨¦n la acertada elecci¨®n del nombre, pues el alquerque es un destacado ejemplo de la versatilidad y el potencial pedag¨®gico de algunos juegos de tablero.

Seg¨²n el n¨²mero de fichas de cada bando, hay tres modalidades b¨¢sicas: alquerque de tres (homologable al popular tres en raya), alquerque de nueve (homologable al molino) y alquerque de 12.

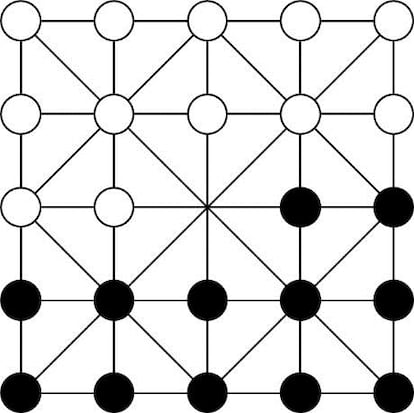
En la figura vemos la posici¨®n de partida del alquerque de 12. Los jugadores, por turno, llevan una de sus fichas a un punto de intersecci¨®n vac¨ªo o, si pueden, ¡°comen¡± una ficha contraria saltando sobre ella a un punto vac¨ªo. Gana quien captura todas las fichas contrarias o les impide mover. En el siglo XV, el alquerque de 12 se fusion¨® con el tablero de ajedrez y dio lugar a las damas. Invito a mis sagaces lectoras/es a llevar las 24 fichas del alquerque sobre el tablero de 8x8 manteniendo la estructura del juego. No sin antes calcular el n¨²mero de jugadas posibles en el primer movimiento, en el segundo, en el tercero¡­ ?Se vislumbra alguna estrategia ganadora?

No solo las damas se derivan del alquerque, sino tambi¨¦n otros juegos de tablero, como el molino (id¨¦ntico al alquerque de nueve en una de sus versiones), m¨¢s conocido como Morris (o nueve hombres de Morris) en el mundo angloparlante. Pero se acaba el espacio-tiempo de la secci¨®n y habr¨¢ que dejarlo para la pr¨®xima entrega.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.