La mosca de Descartes

Con respecto a las elipses de Steiner, vistas la semana pasada, comenta Salva Fuster: ¡°El tri¨¢ngulo cuyos v¨¦rtices son los puntos medios de los segmentos del tri¨¢ngulo original es semejante al original, siendo la raz¨®n de semejanza entre ambos de 1/2 (1/4 si nos referimos al ¨¢rea). Como el baricentro de ambos tri¨¢ngulos es el mismo y las medianas de ambos tri¨¢ngulos coinciden sobre las mismas rectas, la proporci¨®n de ¨¢reas entre las dos elipses ser¨¢ de 1/4, aunque me parece que faltar¨ªa demostrar la unicidad de la inelipse y tambi¨¦n que, construida como semejante a la circunelipse, es tangente a los puntos medios de los segmentos del tri¨¢ngulo original¡±.

Esto es m¨¢s f¨¢cil de comprobar en el caso particular de que el tri¨¢ngulo sea equil¨¢tero, comparando los ejes de ambas elipses y viendo que los de la circunelipse son el doble de los de la inelipse (cuya ¨¢rea es ¦Ð/3¡Ì3 para un tri¨¢ngulo de ¨¢rea 1).

En cuanto a la fracci¨®n 13/42 que, multiplicada por 15!, da el n¨²mero total de soluciones del problema de las colegialas, es el resultado de la siguiente suma:

1/168 + 1/168 + 1/24 + 1/24 + 1/12 + 1/12 + 1/21 = 13/42 (?por qu¨¦?).

Un genio papando moscas

Como vimos la semana pasada, Jakob Steiner detestaba la geometr¨ªa anal¨ªtica, que consideraba ¡°impura¡±, un notable ejemplo de que los matem¨¢ticos, a menudo considerados el paradigma del pensamiento l¨®gico, pueden incurrir en aut¨¦nticos delirios emocionales. Pues la geometr¨ªa anal¨ªtica, con su fusi¨®n del ¨¢lgebra y la geometr¨ªa ¡°pura¡±, es una de las m¨¢s poderosas herramientas matem¨¢ticas.

Los antecedentes se remontan a la antigua Grecia, pues tanto Menecmo, disc¨ªpulo de Plat¨®n, como Apolonio de Perga, el Gran Ge¨®metra, utilizaron m¨¦todos mixtos muy pr¨®ximos a la geometr¨ªa anal¨ªtica tal como hoy la entendemos; aunque el precursor m¨¢s claro fue el insigne poeta y matem¨¢tico persa Omar Jayam, cuyo Tratado sobre demostraciones de problemas de ¨¢lgebra, escrito en el siglo XI, puede considerarse el texto fundacional de la geometr¨ªa anal¨ªtica. Pero quien le dio forma definitiva fue Ren¨¦ Descartes, con ayuda de una mosca.

Debido a su precaria salud, Descartes pasaba mucho tiempo acostado, y no solo salieron de su postraci¨®n sus conocidas reflexiones filos¨®ficas, sino tambi¨¦n algunas importantes aportaciones a la matem¨¢tica. Se cuenta que un d¨ªa yac¨ªa en la cama con la mirada perdida cuando se fij¨® en una mosca que revoloteaba por la habitaci¨®n, y en vez de limitarse a ¡°papar moscas¡±, como habr¨ªa hecho otro, pens¨® que para determinar la posici¨®n del insecto bastaba con conocer su distancia al suelo y a dos paredes perpendiculares entre s¨ª (y al suelo, naturalmente). Y si en vez de revolotear por la habitaci¨®n, la mosca hubiera caminado sobre la mesilla de noche de Descartes, presumiblemente rectangular, podr¨ªa haber determinado su posici¨®n por su distancia a dos lados perpendiculares. Hab¨ªan nacido las coordenadas cartesianas.

La potencia de esta idea tan sencilla estriba en que, tomando como sistema de referencia un par de rectas perpendiculares, podemos convertir una l¨ªnea en una ecuaci¨®n y viceversa. Por ejemplo, la recta de la figura pasa por el punto de intersecci¨®n de los ejes y cualquiera de sus puntos dista del eje horizontal el doble de lo que dista del eje vertical. Llamemos x (abscisa) a la segunda distancia e y (ordenada) a la primera, y todos los puntos de la recta cumplir¨¢n la relaci¨®n y = 2x. O lo que es lo mismo: la recta es la representaci¨®n gr¨¢fica de la ecuaci¨®n y = 2x.

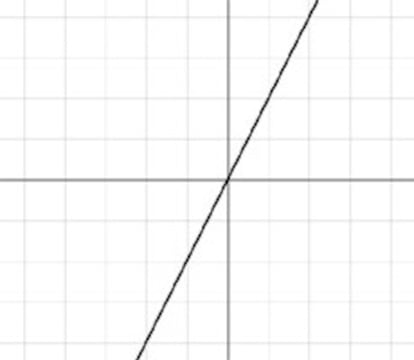
Sin rebuscar en la red ni desempolvar tus viejos libros escolares, ?puedes hallar la ecuaci¨®n de una circunferencia cuyo centro coincide con el punto de intersecci¨®n de los ejes y cuyo radio mide 5 unidades?

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.