C¨®mo estudiar sistemas de muchas dimensiones

Vivimos en un mundo de tres dimensiones espaciales y una dimensi¨®n temporal. Esto significa que, para determinar una ubicaci¨®n exacta en la Tierra en cierto momento, solo necesitamos cuatro valores: las tres coordenadas ¡ªlatitud, longitud y altitud¡ª, y una marca de tiempo. En el universo matem¨¢tico, el concepto de dimensi¨®n es mucho m¨¢s general y es habitual trabajar con sistemas de muchas dimensiones o incluso dimensi¨®n infinita.

Esta noci¨®n no tiene nada que ver con la idea ¡ªtan cultivada en la ciencia ficci¨®n¡ª de universos paralelos, donde se desarrolla una realidad alternativa ajena a nuestra percepci¨®n. Matem¨¢ticamente, las dimensiones son un constructo te¨®rico que describe, simplemente, diversas facetas de algo. En la mec¨¢nica ¡ªla rama de la f¨ªsica que estudia el movimiento y las fuerzas que lo generan¡ª, las dimensiones son la cantidad de informaci¨®n necesaria para describir un sistema. Por ejemplo, un p¨¦ndulo puede verse como un sistema ¡ªllamado espacio de fases¡ª de dos dimensiones, ya que para describir el movimiento del p¨¦ndulo en cualquier instante solo hace falta conocer el ¨¢ngulo que forma la cuerda con respecto a la vertical y la velocidad ¡ªo el momento¡ª.

Para describir sistemas f¨ªsicos m¨¢s complejos, con m¨¢s cuerpos o con m¨¢s iteraciones, es necesario recurrir a espacios de fases m¨¢s complicados, como los que modelizan un sistema planetario, por ejemplo. Estos espacios tienen una estructura geom¨¦trica concreta, llamada variedad simpl¨¦ctica. Estudiar estas variedades y sus propiedades ha sido un tema de inter¨¦s en diversas ¨¢reas de la matem¨¢tica y la f¨ªsica, entre ellas, la llamada mec¨¢nica geom¨¦trica.

La mec¨¢nica geom¨¦trica trata de las aplicaciones de la geometr¨ªa a la mec¨¢nica y permite reducir complicados sistemas de muchas dimensiones ¡ªcomo las variedades simpl¨¦cticas¡ª a otros con los que es m¨¢s f¨¢cil trabajar, ya que, en lugar de observar cada interacci¨®n o movimiento de forma separada, se observan las caracter¨ªsticas globales del sistema y se hace uso de ellas para transformar el problema en otro m¨¢s sencillo.

Para ello, el primer paso es identificar las ¡°simetr¨ªas¡± del sistema, es decir, las transformaciones que lo dejan invariante. Con ellas, es posible reducirlo y as¨ª estudiarlo de forma m¨¢s sencilla, tal y como propon¨ªa Emmy Noether en su famoso teorema. Si el teorema de Noether relaciona cada simetr¨ªa del sistema con una cantidad conservada, la llamada aplicaci¨®n momento, incorpora, a la vez, todas estas relaciones ¡ªsimetr¨ªa/cantidad conservada¡ª del sistema.

A principios de la d¨¦cada de 1980, varios investigadores se dieron cuenta de que, adem¨¢s, esta aplicaci¨®n permit¨ªa traducir el espacio de fases en un objeto m¨¢s sencillo, llamado politopo, que son la generalizaci¨®n a cualquier dimensi¨®n de los pol¨ªgonos. Estas formas tan sencillas ¡ªy discretas¡ª permit¨ªan, por tanto, interpretar propiedades de sistemas muy complicados. Funcionan de forma parecida a Google Maps: ofrecen una imagen, plana y muy f¨¢cil de entender, para representar un mundo, complejo y con m¨¢s dimensiones, al que nos enfrentamos.

Un ejemplo de politopo es el rect¨¢ngulo de la imagen inferior. Representa un sistema formado por tres objetos que se mueven en relaci¨®n los unos con los otros, en un espacio de ocho dimensiones. En particular, indica cu¨¢ndo estos tres objetos se mueven de manera alineada, en ¨¢ngulo recto y cu¨¢ndo el espacio reducido del sistema ¡ªes decir, el que obtenemos tras aplicar nuestro conocimiento sobre las simetr¨ªas¡ª es una esfera u otra forma geom¨¦trica. Adem¨¢s, muestra cuando los tres cuerpos se mueven de una manera estable o m¨¢s ca¨®tica.

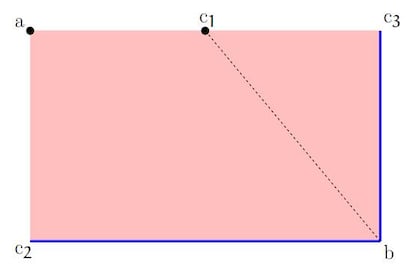
Este politopo, propuesto en resultados recientes de investigaci¨®n, est¨¢ relacionado con sistemas que aparecen en investigaci¨®n en rob¨®tica, termodin¨¢mica y teor¨ªa de campos multidimensional. Efectivamente, uno de los motivos del ¨¦xito de la mec¨¢nica geom¨¦trica es que tiene numerosas aplicaciones: se usa para el dise?o de misiones interplanetarias, en anatom¨ªa computacional, en el dise?o de veh¨ªculos submarinos, de sat¨¦lites, en rob¨®tica, en telecomunicaciones, en el estudio del calentamiento global... La lista es enorme.

Amna Shaddad es investigadora Marie Curie en el Instituto de Ciencias Matem¨¢ticas (ICMAT)

?gata Tim¨®n G Longoria es coordinadora de la Unidad de Cultura Matem¨¢tica del ICMAT

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n y coordinaci¨®n: ?gata A. Tim¨®n G Longoria (ICMAT).

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.