As¨ª se descubrieron mosaicos de variedad infinita con una sola pieza

Los teselados forman uno de los m¨¢s fecundos puntos de encuentro entre las matem¨¢ticas y el arte. Estos recubrimientos del plano por copias de una o varias formas (las piezas, o teselas) constituyen t¨¦cnicas decorativas usadas por numerosas culturas desde la antig¨¹edad. Entre los ejemplos m¨¢s bellos se hallan los mosaicos que adornan varios patios y salones de la Alhambra, y que inspiraron a quien fue uno de los m¨¢s creativos exploradores del potencial est¨¦tico y matem¨¢tico de los teselados: Maurits C. Escher.

Tras siglos de estudio de estas construcciones geom¨¦tricas, decir algo novedoso acerca de los teselados podr¨ªa parecer improbable. Sin embargo, esto es precisamente lo que consiguieron cuatro investigadores en 2023: descubrieron un nuevo tipo de teselas, cuya existencia hab¨ªa sido objeto de especulaciones desde hac¨ªa m¨¢s de medio siglo. Se trata de las llamadas monoteselas aperi¨®dicas, o, como las apod¨® el matem¨¢tico Ludwig Danzer, las einstein (del alem¨¢n ein stein, que significa ¡°una piedra¡±).

Una colecci¨®n de piezas planas permite formar un teselado si es posible cubrir todo el plano pegando copias de estas piezas de forma que no se solapen ni quede ning¨²n hueco entre ellas. Antes de pegar cada pieza, se puede desplazar con movimientos de tres tipos en el plano: traslaciones, rotaciones y reflexiones (es decir, dar la vuelta a la pieza para pegarla por su otra cara).

Entre los ejemplos m¨¢s sencillos se encuentran los teselados regulares, formados a partir de una ¨²nica pieza que es un pol¨ªgono regular. Se sabe, al menos desde los trabajos de Johannes Kepler recogidos en su famosa obra Harmonices Mundi (de 1619), que solo tres pol¨ªgonos regulares permiten construir este tipo de teselado: el tri¨¢ngulo equil¨¢tero, el cuadrado y el hex¨¢gono regular.

Si en la colecci¨®n inicial hay varias piezas distintas, de tipos m¨¢s generales (como pol¨ªgonos no regulares, o incluso formas curvadas), entonces se puede obtener una infinitud de diversos teselados, que dan lugar a m¨²ltiples exploraciones art¨ªsticas, como en los ejemplos de la Alhambra. No obstante, muchos de estos teselados tienen una complejidad limitada, en el sentido de que se repiten, son peri¨®dicos. Un teselado es peri¨®dico si incluye una regi¨®n que permite, traslad¨¢ndola, obtener la totalidad del teselado (sin rotaciones ni reflexiones). Un teselado que no tiene esta propiedad se llama teselado no-peri¨®dico.

Con algunas formas, como el hex¨¢gono regular, solo se pueden hacer teselados peri¨®dicos. Por otro lado, hay formas que pueden generar teselados peri¨®dicos y tambi¨¦n no-peri¨®dicos. Por ejemplo, con un rect¨¢ngulo de proporciones 2:1, podemos hacer un teselado peri¨®dico y otro no-peri¨®dico. Surge entonces la pregunta de si existen colecciones finitas de piezas que solo permiten hacer teselados no-peri¨®dicos. Tales piezas se llamar¨ªan teselas aperi¨®dicas.

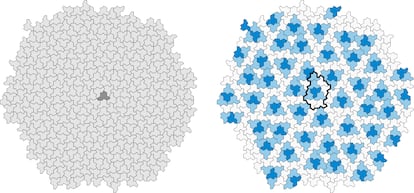
Resulta que s¨ª existen. Se empezaron a conocer ejemplos concretos solo a partir de los a?os sesenta, cuando Robert Berger ¨Den su tesis doctoral en 1964¨D dio una colecci¨®n de 20.426 piezas que, conjuntamente, solo permiten crear teselados no-peri¨®dicos. Este avance inici¨® una intensa b¨²squeda, por varios matem¨¢ticos, de colecciones de teselas aperi¨®dicas con el m¨ªnimo n¨²mero posible de piezas. En 1974, el f¨ªsico y matem¨¢tico Roger Penrose consigui¨® ¨Dinspir¨¢ndose en parte en los trabajos de Kepler¨D hallar una colecci¨®n de teselas aperi¨®dicas con solo dos piezas, estableciendo as¨ª lo que fue el r¨¦cord durante casi medio siglo. Perdur¨® desde entonces el enigma de si existe alguna monotesela aperi¨®dica, es decir, una sola pieza que permite teselar el plano ¨²nicamente de modo no-peri¨®dico.

En 2023, David Smith, Joseph S. Myers, Craig S. Kaplan, y Chaim Goodman-Strauss, dieron con una pieza de este tipo. La primera monotesela aperi¨®dica que descubrieron tiene una forma tan simple que dej¨® at¨®nitos a muchos expertos en este tema. Consiste en un pol¨ªgono de 13 lados, que pronto fue bautizado por sus descubridores como el sombrero. Ahondando en su estudio, los autores descubrieron tambi¨¦n que, lejos de ser ¨²nica, esta forma es solo una de entre una infinitud de posibles formas que tambi¨¦n constituyen monoteselas aperi¨®dicas.

Este descubrimiento no puso fin a esta l¨ªnea de investigaci¨®n, sino que pronto surgieron nuevas cuestiones. Por ejemplo, en el teselado del sombrero se usan todas las tres operaciones permitidas para cubrir el plano: traslaci¨®n, rotaci¨®n y reflexi¨®n. Esto dio lugar a la pregunta de si existen monoteselas aperi¨®dicas cuyos teselados solo usan traslaci¨®n y rotaci¨®n. Los mismos cuatro investigadores descubrieron otra nueva forma geom¨¦trica que dio respuesta positiva a esta pregunta.

M¨¢s all¨¢ de las matem¨¢ticas, las teselas aperi¨®dicas tienen inter¨¦s en f¨ªsica y qu¨ªmica, especialmente por su relaci¨®n con las estructuras llamadas cuasicristales. Los cuasicristales fueron descubiertos por el cient¨ªfico Dan Shechtman en los a?os ochenta, en trabajos que le valieron el Premio Nobel de Qu¨ªmica en 2011. Pocos a?os despu¨¦s de su descubrimiento, se empezaron a estudiar conexiones entre ciertos tipos de cuasicristales y los teselados de Penrose.

Pablo Candela es cient¨ªfico titular del CSIC en el Instituto de Ciencias Matema?ticas (ICMAT).

Caf¨¦ y Teoremas es una secci¨®n dedicada a las matem¨¢ticas y al entorno en el que se crean, coordinado por el Instituto de Ciencias Matem¨¢ticas (ICMAT), en la que los investigadores y miembros del centro describen los ¨²ltimos avances de esta disciplina, comparten puntos de encuentro entre las matem¨¢ticas y otras expresiones sociales y culturales y recuerdan a quienes marcaron su desarrollo y supieron transformar caf¨¦ en teoremas. El nombre evoca la definici¨®n del matem¨¢tico h¨²ngaro Alfred R¨¦nyi: ¡°Un matem¨¢tico es una m¨¢quina que transforma caf¨¦ en teoremas¡±.

Edici¨®n, traducci¨®n y coordinaci¨®n: ?gata Tim¨®n Garc¨ªa-Longoria. Es coordinadora de la Unidad de Cultura Matem¨¢tica del Instituto de Ciencias Matem¨¢ticas (ICMAT)