Teselaciones posibles e imposibles

La paradoja impl¨ªcita en la afirmaci¨®n de que un n¨²mero es ¡°poco interesante¡±, mencionada la semana pasada en relaci¨®n con la famosa an¨¦cdota de Hardy y Ramanujan, es la siguiente: supongamos que algunos de los n¨²meros naturales (enteros y positivos) son interesantes -porque poseen alguna propiedad distintiva- y otros no; el menor de los segundos tendr¨ªa la propiedad distintiva de ser el primero de los no interesantes, y eso lo volver¨ªa interesante, por lo que habr¨ªa que pasarlo al otro grupo. Pero entonces habr¨ªa un nuevo no interesante que ser¨ªa el menor de ellos¡­ Y de este modo, uno tras otro, todos los no interesantes acabar¨ªan en el grupo de los interesantes.

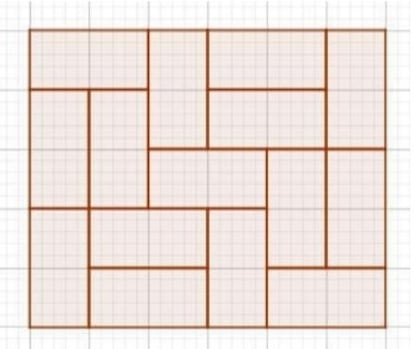
En cuanto al m¨ªnimo rect¨¢ngulo sin l¨ªneas de fractura que se puede formar con domin¨®s es el de 6x5, como el de la figura adjunta (invito a mis sagaces lectoras/es a descubrir otras composiciones, ya sea con fichas de domin¨® o en una hoja de papel cuadriculado). Sobre la imposibilidad de componer un cuadrado de 6x6 sin l¨ªneas de fractura, Manuel Amor¨®s comenta lo siguiente:

¡°La primera observaci¨®n que har¨ªa es que, si una l¨ªnea atraviesa alguna ficha, lo har¨¢, por cuesti¨®n de paridad, a un n¨²mero par de ellas (ya que para llenar una fila o columna lo tienes que hacer con un n¨²mero cualquiera de fichas en su direcci¨®n y un n¨²mero par en la direcci¨®n transversal). Eso significa que cada l¨ªnea que atraviese fichas atravesar¨¢ al menos 2 de ellas. Como en total tenemos 10 l¨ªneas (5 horizontales y 5 verticales), al menos 20 fichas deber¨ªan ser atravesadas en el supuesto de que todas lo fuesen alguna vez. Pero esto es imposible, dado que solo hay 18 fichas. Luego debe haber alguna l¨ªnea que no cortar¨¢ ninguna ficha¡±.

Otro asiduo comentarista, Luca Tanganelli, ha aportado una elegante prueba constructiva de que todo cuadrado de lado par mayor que 6 es teselable sin fracturas:

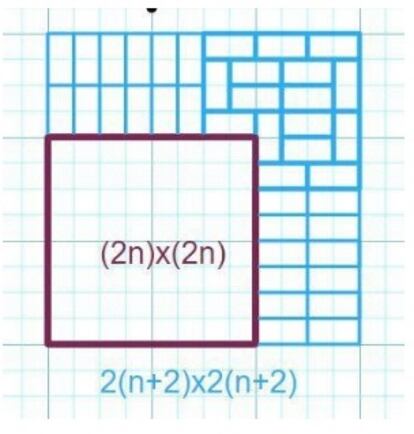
¡°Suponemos que es posible para (2n)x(2n). Entonces en torno a dicho cuadrado se colocan fichas como muestra la imagen. Lo importante es la esquina final superior derecha. Entonces el cuadrado resultante ser¨¢ de 2(n+2)x2(n+2) y sin fracturas. Lo que hay que hacer es simplemente hallar un cuadrado de 8x8 y otro de 10x10 para as¨ª cubrir todos los casos posibles mediante la inducci¨®n, pero tales cuadrados no son dif¨ªciles de encontrar¡±.

Y Salva Fuster env¨ªa la siguiente generalizaci¨®n:

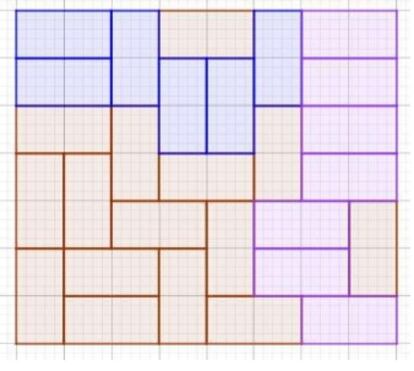
¡°Me parece que esta imagen captura la generalizaci¨®n para cualquier tatami nxm, siendo n impar mayor o igual que 5 y m par mayor o igual que 6. Y lo mismo se podr¨ªa hacer para el caso del tatami con ambos lados pares. Quiz¨¢ haya alguna manera m¨¢s sencilla de verlo, pero creo que con la siguiente imagen ya se ve claro c¨®mo hacerlo. La clave es el tatami 5x6 y c¨®mo extender uno de los lados, o ambos simult¨¢neamente, repitiendo el patr¨®n¡±.

Pasando de los domin¨®s a los tromin¨®s, en la figura vemos una forma de recubrir un tablero de ajedrez (o sea, de 8x8) con 21 tromin¨®s rectos dejando, obviamente, una casilla sin cubrir, ya que 64 no es divisible por 3.

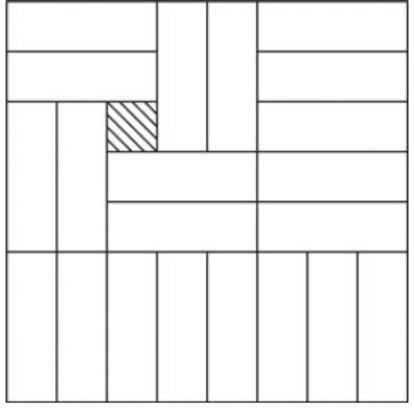
Pero ?y si la casilla sin recubrir es otra? ?En qu¨¦ otros lugares -adem¨¢s del mostrado en la figura- puede quedar la casilla sin cubrir? Concretamente, ?podemos recubrir con 21 tromin¨®s rectos un tablero de ajedrez al que le hemos amputado una de las esquinas?

Este ¨²ltimo rompecabezas puede considerarse una variante de un cl¨¢sico de los problemas de paridad que pide recubrir con 31 fichas de domin¨® un tablero de ajedrez al que se le han quitado las casillas de dos esquinas opuestas; un acertijo sobradamente conocido, pero de obligada menci¨®n en este contexto.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal