Sin l¨ªneas de fractura

El famoso n¨²mero de Ramanujan, como vimos la semana pasada, es el menor que puede expresarse de dos maneras distintas como suma de dos cubos: 1729 = 12? + 1? = 10? + 9?; pero solo si especificamos que estamos hablando de n¨²meros naturales, es decir, enteros y positivos, pues si tambi¨¦n tenemos en cuenta los enteros negativos hay infinitos menores que 1729 que cumplen la condici¨®n (sin ir m¨¢s lejos, ¨C1729).

Por otra parte, la afirmaci¨®n de Hardy de que el n¨²mero era poco interesante entra?a en s¨ª misma una paradoja, se?alada en su d¨ªa por el maestro Martin Gardner, independientemente de la propiedad observada por Ramanujan. ?Qu¨¦ paradoja?

La relaci¨®n cuantitativa entre los poliomin¨®s y los esquemas de Young no ha suscitado comentarios entre los lectores, por lo que la cuesti¨®n queda pendiente.

Mosaicos de poliomin¨®s

Y hablando de Martin Gardner y de poliomin¨®s, recordemos que, aunque fue Solomon W. Golomb quien los ¡°bautiz¨®¡± a mediados del siglo pasado, fue Gardner quien los populariz¨® en su secci¨®n de juegos matem¨¢ticos de Scientific American, y que uno de los problemas que plante¨® fue el de las l¨ªneas de fractura. Por ejemplo, en la figura vemos un rect¨¢ngulo de 5x12, formado por cinco pentomin¨®s, en el que no hay ninguna l¨ªnea de fractura, es decir, ninguna recta horizontal o vertical que vaya de lado a lado, y que en el caso de tratarse de una construcci¨®n f¨ªsica representar¨ªa una debilidad estructural.

En los dos tatamis siguientes, sin embargo, tanto en el de 4x4 como en el de 6x6, hay dos l¨ªneas de fractura verticales.

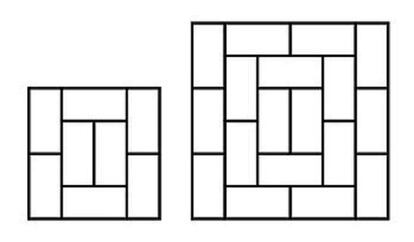
?Podr¨ªan reordenarse sus piezas de manera que no hubiese tales l¨ªneas de fractura? Y en el caso de que no sea posible, ?c¨®mo se puede demostrar tal imposibilidad?

En el caso del tatami de 4x4, la imposibilidad se hace evidente tras unos cuantos intentos, pero en el de 6x6 no es tan obvia, y el propio Golomb dio una elegante demostraci¨®n que invito a mis sagaces lectores a intentar emular (o mejorar, llegado el caso). Cabe preguntarse, dada la imposibilidad en el caso de 6x6, cu¨¢l es el rect¨¢ngulo de m¨ªnimo tama?o y sin l¨ªneas de fractura que puede formarse con domin¨®s. Y una vez hallado este rect¨¢ngulo m¨ªnimo, ?podemos usarlo como punto de partida para, a?adi¨¦ndole los domin¨®s necesarios, formar un cuadrado de 8x8 (es decir, un recubrimiento del tablero de ajedrez) sin l¨ªneas de fractura?

Evidentemente, para que un rect¨¢ngulo pueda ser recubierto por domin¨®s, su ¨¢rea (tomando como unidad el lado menor de un domin¨®) ha de ser par, y para que pueda recubrirse sin l¨ªneas de fractura sus dos lados han de ser mayores de 4. Se puede demostrar (?c¨®mo?) que todos los rect¨¢ngulos y cuadrados que cumplen ambos requisitos pueden ser recubiertos con domin¨®s sin l¨ªneas de fractura, con la ¨²nica y notable excepci¨®n del cuadrado de 6x6.

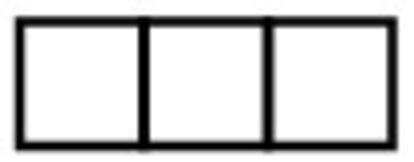
A partir de estas consideraciones, quienquiera que posea un juego de fichas de domin¨® podr¨¢ darle un nuevo e instructivo uso. Y quien se atreva a ir un paso m¨¢s all¨¢ puede experimentar con los tromin¨®s, intentado descubrir, por ejemplo, cu¨¢l es el rect¨¢ngulo m¨ªnimo que puede recubrirse con tromin¨®s rectos (o sea, rect¨¢ngulos de 1x3) sin l¨ªneas de fractura.

Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal