Grafos
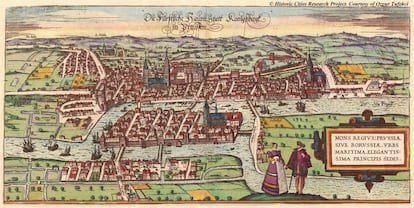
Euler introdujo la teor¨ªa de grafos al analizar el famoso problema de los puentes de K?nigsberg
Las sucesiones at¨ªpicas de la semana pasada podr¨ªan continuar de estas maneras (pero tambi¨¦n de otras):
2, 10, 12, 16, 17, 18, 19, 200, 201, 202¡
1, 2, 3, 4, 7, 10, 17, 24, 41, 58¡
Huevo, gallina, vaca, mosca, ara?a¡
Esponja, avestruz, canguro, dingo, estrella de mar¡
Fresa, mandarina, lim¨®n, uva, ar¨¢ndano¡
Enero, marzo, abril, junio, julio
Do, fa, la, mi, re, si, sol
Fa, la, re, mi, si, do, sol
Dejo a la sagacidad de mis lectoras/es descubrir el criterio de continuidad en cada caso. Dos pistas: la ilustraci¨®n de la semana pasada remite a una de las sucesiones, y los puntos suspensivos indican que la sucesi¨®n podr¨ªa seguir (mientras que si no hay puntos suspensivos significa que la lista est¨¢ completa).
Con respecto a los profetas menores, nadie ha aventurado ninguna hip¨®tesis relativa a sus dos ordenaciones distintas (la primera corresponde a la Biblia jud¨ªa y cat¨®lica, y la segunda a la Septuaginta o Biblia griega), por lo que la cuesti¨®n sigue abierta.
El grafo perdido y hallado
En cuanto al problema tomado del estupendo libro de Clara Grima En busca del grafo perdido (un libro que empiezas pensando: ¡°?Por qu¨¦ no lo habr¨¦ escrito yo?¡± y acabas reconociendo que es mejor que lo haya hecho ella), la soluci¨®n es que Alicia ha dado la mano a 4 personas, como es f¨¢cil ver dibujando el grafo correspondiente.
Recordemos que un grafo es un conjunto de puntos, llamados v¨¦rtices o nodos, unidos por una serie de l¨ªneas, llamadas lados o aristas, que representan relaciones binarias entre los elementos de un conjunto. Si desde cualquiera de los puntos del grafo se puede ir a cualquier otro recorriendo aristas, es un grafo conexo. Y si en un grafo conexo no hay circuitos cerrados, se denomina ¨¢rbol, por su semejanza con los ¨¢rboles de la naturaleza (el ?rbol de la Ciencia de Ram¨®n Llull y el ?rbol de Porfirio son ilustres precursores de los grafos arb¨®reos).
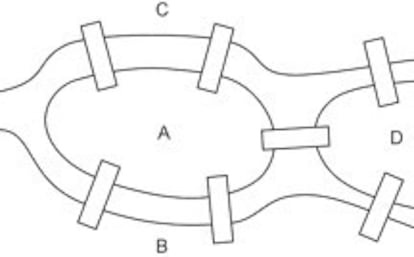
Se puede considerar que la teor¨ªa de grafos la inaugur¨® Euler en 1736 con un art¨ªculo sobre el famoso problema de los puentes de K?nigsberg (la actual Kaliningrado), del que nos hemos ocupado en alguna ocasi¨®n, en el que demostraba que era imposible recorrer las cuatro zonas de la ciudad pasando por sus siete puentes una sola vez y regresando al punto de partida.
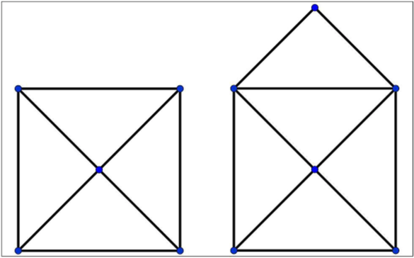
Otro conocido problemas de grafos es el de dibujar un sobre abierto sin levantar el l¨¢piz del papel ni pasar dos veces por el mismo trazo. ?Es posible? ?Y si el sobre est¨¢ cerrado?
Volviendo al libro de Clara Grima, en uno de sus cap¨ªtulos habla del pol¨¦mico (algunos consideran que ha sido demostrado y otros opinan que no del todo) teorema topol¨®gico de los cuatro colores, que afirma que cuatro colores son suficientes para colorear cualquier mapa de manera que nunca dos zonas lim¨ªtrofes sean del mismo color. Cuatro colores son suficientes, pero no siempre necesarios; por ejemplo, para colorear de esta manera un tablero de ajedrez bastan dos colores.
Y para colorear el mapa de Andaluc¨ªa de forma que sus ocho provincias queden claramente diferenciadas (es decir, sin que dos provincias fronterizas sean del mismo color), ?son necesarios cuatro colores o se puede lograr con menos? ?Y para colorear el mapa de la Espa?a peninsular? (Versi¨®n f¨¢cil: dividido en comunidades aut¨®nomas; versi¨®n menos f¨¢cil: dividido en provincias).
Carlo Frabetti es escritor y matem¨¢tico, miembro de la Academia de Ciencias de Nueva York. Ha publicado m¨¢s de 50 obras de divulgaci¨®n cient¨ªfica para adultos, ni?os y j¨®venes, entre ellos ¡®Maldita f¨ªsica¡¯, ¡®Malditas matem¨¢ticas¡¯ o ¡®El gran juego¡¯. Fue guionista de ¡®La bola de cristal¡¯.
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.
Tu suscripci¨®n se est¨¢ usando en otro dispositivo
?Quieres a?adir otro usuario a tu suscripci¨®n?
Si contin¨²as leyendo en este dispositivo, no se podr¨¢ leer en el otro.
FlechaTu suscripci¨®n se est¨¢ usando en otro dispositivo y solo puedes acceder a EL PA?S desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripci¨®n a la modalidad Premium, as¨ª podr¨¢s a?adir otro usuario. Cada uno acceder¨¢ con su propia cuenta de email, lo que os permitir¨¢ personalizar vuestra experiencia en EL PA?S.
?Tienes una suscripci¨®n de empresa? Accede aqu¨ª para contratar m¨¢s cuentas.
En el caso de no saber qui¨¦n est¨¢ usando tu cuenta, te recomendamos cambiar tu contrase?a aqu¨ª.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrar¨¢ en tu dispositivo y en el de la otra persona que est¨¢ usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aqu¨ª los t¨¦rminos y condiciones de la suscripci¨®n digital.
Sobre la firma































































