Fracciones egipcias

Con respecto al problema de las 100 c¨¢psulas, planteado la semana pasada, he aqu¨ª lo que comenta Piciencia:

¡°En el caso a) el que juega primero puede ganar si elige la c¨¢psula llena, pero a cambio, si no acierta, compensa al que juega segundo al eliminar una c¨¢psula vac¨ªa. En el b) esa compensaci¨®n no se da y el primero tiene una ventaja segura. Que la compensaci¨®n en a) es suficiente como para igualar las probabilidades de los dos jugadores, en la soluci¨®n de MoMath se explica planteando que es un juego equivalente a asignar al principio 50/100 c¨¢psulas a cada uno¡±.

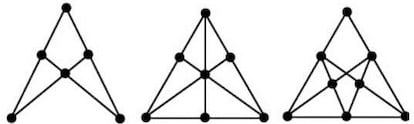
En cuanto al ¡°problema del huerto¡±, no intentes mejorar la configuraci¨®n de la figura de la entrega anterior: con 9 puntos, el m¨¢ximo de alineaciones de 3 puntos obtenibles es 10. Con 3 o 4 puntos, obviamente, solo se puede formar una alineaci¨®n de 3 puntos; con 5 puntos solo se pueden conseguir 2; con 6 puntos, 4; con 7 puntos, 6; con 8 puntos, 7; con 9 puntos, como ya hemos visto, 10¡­ La secuencia, a medida que aumentamos el n¨²mero de puntos a partir de 3, es 1, 1, 2, 4, 6, 7, 10, 12, 16, 19, 22, 26¡­ ?Podemos sacar alguna conclusi¨®n de esta secuencia?

La sucesi¨®n de Sylvester

No podemos despedirnos de James Joseph Sylvester y de sus problemas de alineaci¨®n de puntos sin mencionar la sucesi¨®n que lleva el nombre del gran matem¨¢tico brit¨¢nico.

La sucesi¨®n de Sylvester es una vertiginosa sucesi¨®n de n¨²meros naturales (enteros y positivos) en la cual cada t¨¦rmino es el producto de todos los anteriores m¨¢s 1. Los ocho primeros t¨¦rminos de la sucesi¨®n, que crece de forma doblemente exponencial, son:

2, 3, 7, 43, 1807, 3263443, 10650056950807, 113423713055421844361000443¡­

Obs¨¦rvese que el noveno t¨¦rmino de la sucesi¨®n dif¨ªcilmente cabr¨ªa en una sola l¨ªnea, pues tendr¨ªa¡­ ?cu¨¢ntas cifras?

Es interesante considerar la serie de los inversos de los t¨¦rminos de la sucesi¨®n de Sylvester:

1/2 + 1/3 + 1/7 + 1/43¡­

Es f¨¢cil ver que es una serie convergente (basta compararla con otra serie convergente bien conocida: 1/2 + 1/4 + 1/8 + 1/16¡­ y ver que sus denominadores crecen mucho m¨¢s deprisa), pero ?a qu¨¦ valor converge? Sirva la siguiente figura como pista gr¨¢fica.

La serie de los inversos de la sucesi¨®n de Sylvester (o, m¨¢s exactamente, cualquier subconjunto finito de sus t¨¦rminos) es una fracci¨®n egipcia, es decir, una suma de fracciones unitarias distintas (fracci¨®n unitaria es aquella cuyo numerador es 1 y cuyo denominador es un n¨²mero natural).

Las fracciones egipcias se denominan as¨ª porque los antiguos egipcios las utilizaban recurrentemente en sus c¨¢lculos, como se desprende del papiro de Ahmes (tambi¨¦n conocido como papiro de Rhind) y otros documentos milenarios.

Invito a mis sagaces lectoras/es a viajar al remoto pasado (unos cuatro mil a?os atr¨¢s) para demostrar que cualquier n¨²mero racional puede expresarse como fracci¨®n egipcia. La cuesti¨®n ser¨ªa trivial si se pudieran repetir denominadores (por ejemplo, 3/7 = 1/7 + 1/7 + 1/7); pero hay que tener en cuenta que en las fracciones egipcias todos los denominadores han de ser distintos.

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.