El oso blanco y otros cl¨¢sicos

Sobre el primer problema de ajedrez de la semana pasada, he aqu¨ª lo que comenta nuestro ¡°usuario destacado¡± Salva Fuster:

¡°Respecto al problema ajedrec¨ªstico que propuso Manuel, la m¨¢quina s¨ª que es capaz de hallar el mate en 2 jugadas, pero debemos especificar en la configuraci¨®n que no se le permite el enroque. Es una opci¨®n de configuraci¨®n que el programa podr¨ªa detectar como no v¨¢lida, pero por lo que parece, no se contempla en el algoritmo, pues si las posiciones de la torre y el rey son las de partida, independientemente de que se hayan podido mover, se deja la opci¨®n de permitir el enroque o no¡±.

Detr¨¢s de una gran m¨¢quina que no llega suele haber un humano que se pasa (de listo).

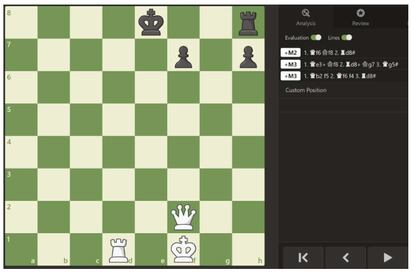
Y a?ade Fuster en otro comentario: ¡°Respecto al problema de Greco, me parece que hay malas noticias para los supremacistas humanos, pues he probado el an¨¢lisis de Stockfish (me parece que la versi¨®n 11, que es mucho menos potente que la actual) y s¨ª que llega a las tablas empezando las negras¡±.

?Y cu¨¢l es la estrategia entabladora de las negras? Su primera jugada est¨¢ clara: 1¡­ Ra1+, salvando as¨ª la torre amenazada y dando jaque. Las blancas intentar¨¢n cambiar piezas para llegar con sus dos peones de ventaja a un final ganador, as¨ª que har¨¢n gustosamente su ¨²nica jugada posible, que es interponer la torre: 2. Rf1¡­ Y, contra todo pron¨®stico, las negras optan por el cambio y juegan 2¡­ Rxf1, capturando la torre blanca. Con ello parecen estar siguiendo la estrategia de las blancas, y sin embargo¡­ Dejo amis sagaces lectoras/es la continuaci¨®n de la famosa partida del Calabr¨¦s.

En el ¨²ltimo problema de la semana pasada, el rey blanco tiene que trasladarse pacientemente hasta f1 para apoyar a la torre en un traslado zigzagueante hasta a1. As¨ª, si un pe¨®n negro come la torre, el rey blanco lo come a su vez y el cambio le favorece, y si la torre no es comida puede abrirse paso por la primera columna al retirarse el alfil blanco.

Osos, balas y balanzas

Y puesto que hemos revisados algunos cl¨¢sicos de los problemas de ajedrez, sigamos en la misma l¨ªnea clasicista. He aqu¨ª tres temas bastante antiguos, pero a los que es posible acercarse de una manera nueva:

1. En este conocido acertijo se suele preguntar de qu¨¦ color es el oso, pero en este caso lo revelar¨¦ de entrada: te encuentras con un oso blanco adormilado y, temiendo que pueda despertar hambriento, huyes hacia el norte. Tras recorrer 10 kil¨®metros en esta direcci¨®n, haces otros 10 hacia el este y luego 10 m¨¢s hacia el sur¡­ y compruebas con horror que has vuelto al punto de encuentro con el oso, que ya no est¨¢ dormido. ?Puedes decir d¨®nde te devorar¨¢?

2. Otro tema cl¨¢sico es el del empaquetamiento de esferas, cuesti¨®n de gran relevancia militar en el pasado: en los parques de artiller¨ªa se sol¨ªan apilar las balas de ca?¨®n esf¨¦ricas en pir¨¢mides de base cuadrada, con 15 balas por lado en el cuadrado de la base. ?Cu¨¢ntas balas hab¨ªa en cada pir¨¢mide? ?Puedes hallar una f¨®rmula general que valga para pir¨¢mides de balas de cualquier tama?o?

3. Las balanzas, precisas o defectuosas, tambi¨¦n dan mucho juego y se prestan a numerosas variantes: en un antiguo mercado persa abundaban las balanzas enga?osas, con un brazo ligeramente m¨¢s largo que el otro, y los clientes pidieron a las autoridades que promulgasen alguna ley que los protegiera de los mercaderes tramposos, de modo que se public¨® un bando seg¨²n el cual las mercanc¨ªas ten¨ªan que pesarse primero en un platillo de la balanza y luego en el otro, y el cliente pagar¨ªa por el promedio de ambas pesadas. ?Era equitativa esta medida?

Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.