Por los caminos de Euler y Hamilton

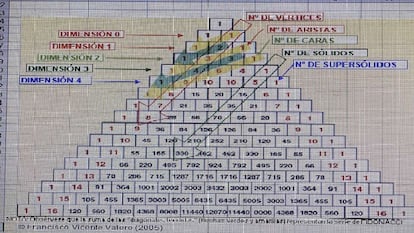
Con respecto a los ¡°tesoros ocultos¡± en el tri¨¢ngulo de Pascal-Tartaglia-Jayam, del que nos ocupamos, una vez m¨¢s, la semana pasada, Francisco Vicente manda, en relaci¨®n con la secuencia de Fibonacci (ver la nota al pie de la imagen), el siguiente gr¨¢fico de creaci¨®n propia:

Y en relaci¨®n con la presencia del n¨²mero e en el tri¨¢ngulo, dice Luca Tanganelli: ¡°Una relaci¨®n del tri¨¢ngulo de Jayam con e que se me ocurre es la siguiente. Se dibuja el tri¨¢ngulo en su forma centrada, haciendo que la distancia que separa dos n¨²meros adyacentes sea igual a la distancia entre l¨ªneas. Despu¨¦s se traza una par¨¢bola que pase por la c¨²spide y por los extremos de la fila 1-2-1. La relaci¨®n entre el valor del tri¨¢ngulo en el eje vertical con respecto al valor del tri¨¢ngulo en la par¨¢bola, a la misma altura, tiende a e¡±. Brillante, pero ?a alguien se le ocurre una relaci¨®n m¨¢s sencilla?

Y Salva Fuster plantea una interesante cuesti¨®n que someto a la consideraci¨®n de mis sagaces lectoras/es: ¡°Busc¨¢ndole tres pies al gato se me ocurre plantear si los n¨²meros decimales formados como 0,... en los que sustituimos los puntos suspensivos por la concatenaci¨®n de cifras de los n¨²meros que forman las diagonales del tri¨¢ngulo, son siempre irracionales (salvo el primero):

0,1111...

0,1234...

0,13610...¡±

Recorridos eulerianos y hamiltonianos

Hace un par de semanas (ver comentarios de 2024 y los n¨²meros tetra¨¦dricos) surgi¨® una moment¨¢nea confusi¨®n entre caminos eulerianos y hamiltonianos, que es un buen pretexto para se?alar la diferencia entre ambos recorridos, que a menudo se consideran equivalentes, aunque no lo son.

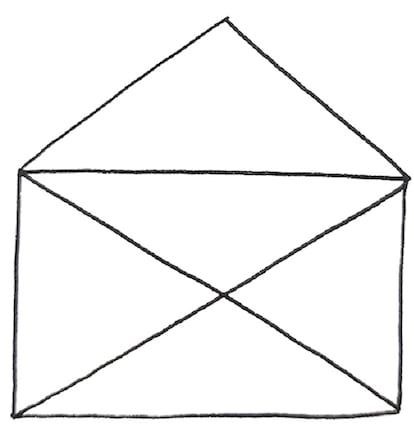
Un camino euleriano recorre todas las aristas de una figura (un grafo, hablando con propiedad matem¨¢tica) pasando solo una vez por cada una de ellas. El t¨ªpico pasatiempo consistente en dibujar una figura (por ejemplo, un sobre abierto) sin levantar el l¨¢piz del papel y sin volver a pasar por una l¨ªnea ya trazada, se resuelve mediante un camino euleriano. Si el camino es cerrado (es decir, si termina en el mismo punto en el que empieza), es un ciclo euleriano. Obs¨¦rvese que en el conocido pasatiempo del sobre abierto s¨ª se puede (y de hecho es inevitable) volver a pasar por un mismo v¨¦rtice, pero no por una misma l¨ªnea.

En el camino hamiltoniano, sin embargo, se trata de pasar por todos los v¨¦rtices una sola vez. Como en el caso anterior, si el camino es cerrado se llama ciclo hamiltoniano. Por supuesto, un camino puede ser a la vez euleriano y hamiltoniano (?qu¨¦ condici¨®n ha de cumplir un camino para ser a la vez euleriano y hamiltoniano?).

Al igual que el recientemente revisitado tri¨¢ngulo de Pascal-Tartaglia, los que conocemos como caminos hamiltonianos ya hab¨ªan sido estudiados mucho antes por los matem¨¢ticos orientales. Ya en el siglo IX, el poeta indio Rudrata habla del ¡°camino del caballo¡±: un recorrido del trebejo saltar¨ªn por todo el tablero pasando una sola vez por cada escaque (?puedes efectuar ese recorrido?, ?ves por qu¨¦ es un camino hamiltoniano?).

Hamilton estudi¨® los recorridos que llevan su nombre en los s¨®lidos plat¨®nicos, y en 1857 permiti¨® que se comercializara un rompecabezas basado en los caminos hamiltonianos, consistente en hallar un recorrido por las aristas de un dodecaedro que pasara una sola vez por todos sus v¨¦rtices (parece ser que las 25 libras que le pagaron en aquella ocasi¨®n fue todo el dinero que Hamilton percibi¨® en su vida por sus hallazgos matem¨¢ticos). Puedes entretenerte resolvi¨¦ndolo sin necesidad de echar mano de un dodecaedro propiamente dicho, o sea, tridimensional: su proyecci¨®n sobre el plano sirve igualmente (as¨ª que la primera parte del problema consiste en dibujar un equivalente topol¨®gico bidimensional del dodecaedro).

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.