2024 y los n¨²meros tetra¨¦dricos

He de empezar subsanando una omisi¨®n: la semana pasada habl¨¦ del 2024 y de los n¨²meros piramidales cuadrados, y no mencion¨¦ que 2024 tambi¨¦n es un n¨²mero piramidal, aunque no cuadrado sino triangular. Afortunadamente, mis amables lectoras/es suelen estar al quite: Javier Tamames me record¨® que 2024 es un n¨²mero tetra¨¦drico (como tambi¨¦n se denominan los n¨²meros piramidales triangulares) e Ignacio Larrosa mand¨® una elocuente visualizaci¨®n en forma de pir¨¢mide triangular de esferas apiladas, cuyos 22 niveles suman 2024.

Una pir¨¢mide cuya base es un tri¨¢ngulo es un tetraedro, y por ello los n¨²meros piramidales triangulares tambi¨¦n se llaman tetra¨¦dricos. Si en la visualizaci¨®n del apilamiento de esferas vamos sumando las de cada nivel, empezando por arriba, obtenemos la secuencia de los n¨²meros tetra¨¦dricos (correspondientes al n¨²mero de esferas de los tetraedros de 1, 2, 3, 4¡­ esferas por cada lado): 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364¡­

Los sucesivos niveles de la pir¨¢mide forman, a su vez, la secuencia de los n¨²meros triangulares (visualizables como tri¨¢ngulos equil¨¢teros de esferas):

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78¡­

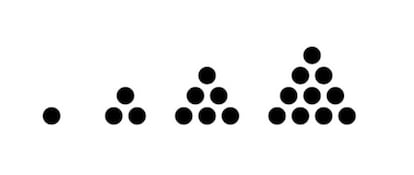
Y, por tanto, el en¨¦simo n¨²mero tetra¨¦drico (Tn) es la suma de los n primeros n¨²meros triangulares:

T1 = 1

T2 = 1 + 3 = 4

T3 = 1 + 3 + 6 = 10

T4 = 1 + 3 + 6 + 10 = 20

T5 = 1 + 3 + 6 + 10 + 15 = 35

¡­

T22 = 1 +3 + 6 + 10 + 15 + 21 + 28¡­ + 210 + 231 + 243 = 2024

?Puedes hallar una f¨®rmula que permita determinar que el vig¨¦simo segundo n¨²mero tetra¨¦drico es 2024 sin necesidad de efectuar la larga suma anterior?

Un poco m¨¢s dif¨ªcil: al cotejar las dos listas anteriores, vemos una coincidencia: el 10, lo que significa que el tercer n¨²mero tetra¨¦drico es igual al cuarto n¨²mero triangular. ?Puedes encontrar m¨¢s n¨²meros que sean a la vez triangulares y tetra¨¦dricos?

M¨¢s dif¨ªcil todav¨ªa: entre los primeros n¨²meros tetra¨¦dricos hay dos que son cuadrados perfectos: 1 y 4. ?Puedes encontrar alguno m¨¢s o demostrar que no existen?

Las cartas de Zener

Adem¨¢s de maestro de divulgadores cient¨ªficos, Martin Gardner fue un implacable desenmascarador de falacias, seudociencias y paranormalidades varias, y a veces usaba ir¨®nicamente los argumentos de los magufos, o sus instrumentos, como materia prima de sus pasatiempos matem¨¢ticos.

En un interesante art¨ªculo tra¨ªdo a colaci¨®n por Manuel Amor¨®s, Gardner parte de las cartas de Zener (hoy ca¨ªdas en un merecido olvido, pero anta?o muy populares), utilizadas para evaluar supuestas capacidades telep¨¢ticas, para plantear un interesante problema de recubrimiento, que ha suscitado un animado debate entre las/os lectoras/es (ver comentarios de la semana pasada).

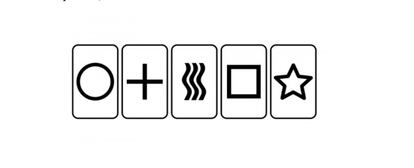
?Cu¨¢les de estos cinco s¨ªmbolos pueden dibujarse ¨¢lef 1 veces sobre un papel, suponiendo que se trazan con l¨ªneas ideales, sin grosor, y que no se solapan ni se cortan entre ellos? Los s¨ªmbolos pueden ser de distintos tama?os, pero han de ser semejantes geom¨¦tricamente. Recordemos que ¨¢lef 1 es el infinito, no numerable, de los n¨²meros reales.

Resulta que todos los s¨ªmbolos menos uno pueden dibujarse ¨¢lef 1 veces. ?Puedes decir cu¨¢l es y por qu¨¦? Una doble pregunta con dos niveles de dificultad, porque es relativamente f¨¢cil demostrar que los cuatro s¨ªmbolos dibujables innumerables (literalmente) veces lo son, con lo que queda identificado, por eliminaci¨®n, el que no lo es. Pero demostrar por qu¨¦ no lo es ya no resulta tan sencillo, y el propio Gardner se limita a esbozar una v¨ªa de resoluci¨®n no del todo clara.

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.