Borges y el infinito

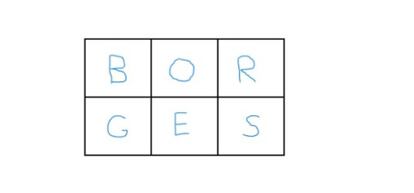
No es posible reconstruir a BORGES a partir de su anagrama nabokoviano OSBERG mediante un plegado del mapa de 2x3 de la semana pasada. Basta con darse cuenta de que la E y la S, que en la palabra BORGES est¨¢n juntas, en la cuadr¨ªcula OSBERG ocupan casillas que solo comparten un v¨¦rtice, y ning¨²n plegado puede conseguir que dos casillas ¡°opuestas por el v¨¦rtice¡± sean adyacentes. Por consiguiente, tampoco se puede pasar de BORGES a OSBERG: en este caso hay dos parejas de letras en casillas opuestas por el v¨¦rtice (B-E y O-S) que en OSBERG van juntas.

En cuanto a las distintas posibilidades de plegado de tr¨ªpticos, pol¨ªpticos y mapas elementales, nuestro comentarista habitual Francisco Montesinos ha llevado a cabo un an¨¢lisis muy detallado (ver comentarios de la semana pasada) que, por razones de espacio, no puedo reproducir entero; esto es lo que dice del mapa elemental de 2x2 (y de paso, entre par¨¦ntesis, alude a la imposibilidad que acabamos de ver):

¡°En el caso 2x2, numerando las hojas (1, 4, 2, 3) de izquierda a derecha y de arriba a abajo se tienen 24 permutaciones, de las que 8 dan configuraciones imposibles (dos p¨¢ginas en posici¨®n diagonal llevar¨¢n alguna intercalada) y de las 16 restantes 8 ser¨¢n sim¨¦tricas, por lo que quedar¨¢n 8 plegamientos diferentes posibles. Otra forma de llegar al mismo resultado es considerando que fijada la primera hoja en vista frontal (4 posibilidades) para la siguiente hay solo 2 posibilidades y solo una para las dos posiciones restantes, 8 en total¡±.

Borges desmantelado

Tras la publicaci¨®n de la anterior entrada de El juego de la ciencia, Borges deconstruido, apareci¨® en Columna Digital un art¨ªculo titulado Borges desmantelado, y cuesta creer que, con pocas horas de diferencia, se publiquen dos textos de t¨ªtulos tan parecidos por pura casualidad. (Invito a mis sagaces lectoras/es a calcular ¡°a la manera de Fermi¡± el orden de magnitud de la probabilidad de que algo as¨ª ocurra aleatoriamente).

En cualquier caso, el citado art¨ªculo dice, entre otras cosas: ¡°En el centro de su obra, Borges coloca la idea del infinito, un concepto que juega un papel crucial tanto en sus narrativas como en sus ensayos. La infinitud de los libros en La Biblioteca de Babel, los espejos que se reflejan eternamente en Tl?n, Uqbar, Orbis Tertius, y los laberintos sin fin son solo algunos ejemplos de c¨®mo Borges desaf¨ªa nuestra comprensi¨®n del tiempo y el espacio, llev¨¢ndonos a cuestionar la realidad misma¡±.

En (la) realidad (misma), ninguna de las tres cosas mencionadas es infinita: el n¨²mero de libros posibles es -aunque inmenso- finito e incluso f¨¢cilmente calculable, como ya mostr¨® el matem¨¢tico y fil¨®sofo alem¨¢n Kurd Lasstwiz (1848-1910) en su pionero relato La biblioteca universal, en el que se inspir¨® Borges para escribir La biblioteca de Babel. Y los espejos que se reflejan el uno en el otro lo hacen tan lentamente -a la exigua, desde el punto de vista astron¨®mico, velocidad de la luz- que el n¨²mero de im¨¢genes que podr¨ªan generar antes de que se extinga el universo no solo no es infinito, sino ni siquiera muy grande comparado con otros monstruos num¨¦ricos (como el de posibles partidas de ajedrez, por ejemplo).

En cuanto a los ¡°laberintos sin fin¡±, ?puede existir tal cosa? ?C¨®mo ser¨ªa un laberinto, como el m¨ªtico de Creta, del que fuera imposible salir? Borges, salvo error u omisi¨®n, no habla en ning¨²n momento de laberintos sin fin, pero s¨ª de ciertos laberintos de los que se sale girando siempre hacia la izquierda. ?C¨®mo ser¨ªa un tal laberinto lev¨®giro?

La peculiar -y un tanto confusa- relaci¨®n del escritor argentino con el infinito hay que buscarla, sobre todo, en sus relatos El Aleph, El jard¨ªn de senderos que se bifurcan y Las ruinas circulares, y tal vez en algunos poemas. No en vano El Aleph lleva el nombre de ¡°la terrible dinast¨ªa¡± de los n¨²meros transfinitos de Cantor¡­ Pero ese es otro art¨ªculo.

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.