El problema de Alhac¨¦n

Con respecto al problema cl¨¢sico de la mesa de billar a una o varias bandas, nuestro comentarista habitual Rafael Granero ha enviado un an¨¢lisis exhaustivo que vale la pena reproducir entero:

Supongamos bolas de billar de radio 1. Supongamos la mesa de billar en un sistema de coordenadas donde el extremo inferior derecho de la mesa est¨¢ en el punto (-1, -1) y el extremo superior derecho en el punto (n3 + 1, m3 + 1). Sabemos las coordenadas de los centros de la bola amarilla (n1, m1) y de la bola roja (n2, m2). Hagamos una imagen especular con respecto el eje de la Y (el eje est¨¢ a una unidad de la banda inferior de la mesa), el centro de esta imagen estar¨¢ en (-n2, m2).

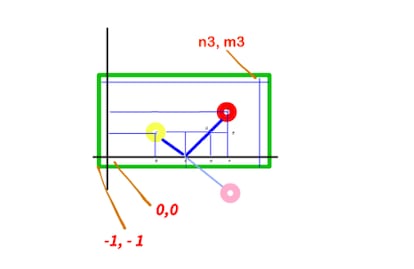
La ecuaci¨®n de la recta que une a los centros de la bola amarilla y la imagen de la bola roja es:

(y2 - y1 )x - (x2 - x1)y + (x2¡¤y1 - x1¡¤y2) = 0

Y dado que el punto A tiene x = 0, entonces y = (-n2¡¤m1 - n1¡¤m2) / (-n2 - n1). Por otra parte, los tri¨¢ngulos ABC y AGD son iguales, y proporcionales a los tri¨¢ngulos AFH y DEH. Por lo que sabiendo la distancia del segmento HE y HF ([n2-n1] y [n2, respectivamente), sabemos la proporci¨®n entre los segmentos DE (y GF) con respecto AF.

Tambi¨¦n sabemos que el segmento BA = AG y que 2AG+GF = m2-m1, y que, por lo anterior dicho sobre los tri¨¢ngulos proporcionales AFH y DEH,

GF/(AG+GF)=(n2-n1)/n2

Despejando GF (o AG) podemos saber los valores de GF y AG (BA) y hallar el y de A (m1 + BA).

En el caso de dos bandas (inferior y derecha) primero hay que crear la imagen especular a la derecha (nuevas coordenadas (n2, 2¡¤m3 - m2)) y luego la imagen especular hacia abajo (-2n, 2¡¤m3 - m2), y con base en la ecuaci¨®n de una recta que une dos puntos, volver a calcular la coordenada y del nuevo punto, ya que seguir¨¢ la x = 0.

En el caso de tres, ser¨¢ necesario tres im¨¢genes especulares para ir convirtiendo una recta quebrada de cuatro segmentos en una recta de un ¨²nico segmento¡­ Y as¨ª, tantas bandas como queramos pensar.

Fotones como bolas de billar

Como se dijo la semana pasada, si planteamos el problema en una mesa de billar circular en lugar de rectangular y queremos averiguar en qu¨¦ punto de la banda tendr¨¢ que incidir una bola para golpear de lleno la otra, tenemos una versi¨®n billar¨ªstica del famoso problema de Alhac¨¦n.

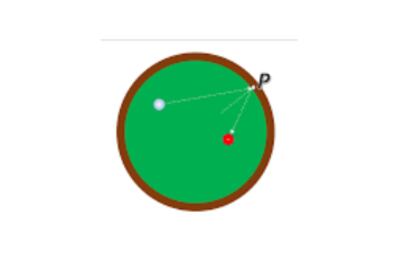
Es f¨¢cil ver que el punto P de incidencia de la bola atacante tendr¨¢ que ser tal que la bisectriz del ¨¢ngulo que determinan los centros de las bolas con P sea perpendicular a la tangente en P (lo que equivale a decir que dicha bisectriz coincide con un di¨¢metro de la mesa circular). Determinar dicho punto en funci¨®n de las posiciones de las dos bolas ya no es tan f¨¢cil, y animo a mis sagaces lectoras/es a abordar el problema desde distintos ¨¢ngulos (nunca mejor dicho): geom¨¦trico, algebraico¡­ El problema se simplifica si ambas bolas est¨¢n sobre un di¨¢metro de la mesa: en ese caso hay una soluci¨®n trivial, que consiste en lanzar una de las bolas contra la banda siguiendo el di¨¢metro que determinan ambas, de forma que la bola atacante vaya y vuelva por el di¨¢metro mismo; pero tambi¨¦n hay otra soluci¨®n (mejor dicho, dos sim¨¦tricas), y hallarla es un primer paso para resolver el problema general, cuando las bolas no est¨¢n sobre un mismo di¨¢metro.

Pero Ibn al-Haytham (965-1040), conocido en Occidente como Alhac¨¦n, como corresponde a quien con toda justicia es considerado el padre de la ¨®ptica (y sobre todo de la cat¨®ptrica, la ¨®ptica de los espejos), no plante¨® su famoso problema sobre una mesa de billar, sino en el interior de un espejo circular, en el que el equivalente de las bolas de marfil son los fotones.

Imag¨ªnate que est¨¢s dentro de una habitaci¨®n circular cuya pared es toda ella reflectante y que con el fino haz de un puntero l¨¢ser quieres iluminar un objeto de la habitaci¨®n, pero no directamente, sino haciendo que el rayo de luz se refleje en la pared: ?con qu¨¦ ¨¢ngulo tendr¨¢s que dirigir el rayo para conseguir tu objetivo? Y una intrigante pregunta off the record: ?c¨®mo ser¨ªa tu imagen reflejada en ese espejo circular envolvente?

Puedes seguir a MATERIA en Facebook, X e Instagram, o apuntarte aqu¨ª para recibir nuestra newsletter semanal.