Todos (s¨ª, TODOS) los mapas planos de la Tierra est¨¢n mal

?Paren las rotativas! ?Notici¨®n! Todos los mapas planos de nuestro querido planeta Tierra que hayamos podido ver en lo que llevamos de vida, y todos los que podamos contemplar en lo que nos queda por aqu¨ª, est¨¢n mal. ?Todos!

?C¨®mo puede ser que ni uno solo de los mapas planos de la Tierra que han existido, existen y existir¨¢n est¨¦ bien? ?Tan malos somos haciendo mapas? No, no va la cosa por ah¨ª. En realidad son las matem¨¢ticas las que tienen la culpa. Bueno, m¨¢s que ¡°culpa¡± lo que tienen es la explicaci¨®n de este curioso hecho.

Antes de adentrarnos en la parte matem¨¢tica, vamos a analizar la situaci¨®n visualmente. Realizando en Google la b¨²squeda ¡°mapa terrestre¡± encontrar¨¦is multitud de mapas planos de nuestro planeta. He tomado algunos de los que aparecen en la primera p¨¢gina de resultados y he rodeado Groenlandia en todos ellos:

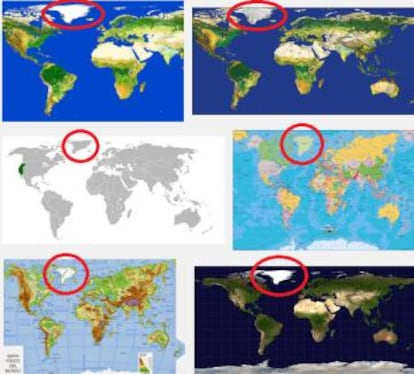
Como pod¨¦is ver, la forma de Groenlandia y su tama?o relativo al resto de territorios no es el mismo en todos los mapas. Pod¨¦is hacer lo mismo con islas, pa¨ªses o continentes: lo m¨¢s probable es que encontr¨¦is diferencias significativas en ellos dependiendo del mapa que est¨¦is consultando.

?C¨®mo se construye un mapa terrestre plano? Pues, suponiendo que la Tierra es una esfera (se acerca lo suficiente a ella como para que esta suposici¨®n sea adecuada), un mapa plano terrestre se construye mediante una proyecci¨®n de cada punto de la esfera terrestre en un plano. Y hay muchas formas de proyectar una esfera en un plano: tenemos proyecciones cil¨ªndricas, proyecciones c¨®nicas, proyecciones azimutales, modificaciones o combinaciones de las mismas¡­

A un mapa plano ¡°perfecto¡± de la Tierra podr¨ªamos pedirle muchas cosas, pero, al menos, deber¨ªa cumplir que, salvo factores de escala, mantenga las ¨¢reas y las distancias y tambi¨¦n que conserve los ¨¢ngulos. Vamos, que las ¨¢reas de los territorios en el mapa plano sean proporcionales a las ¨¢reas en la esfera (y con la misma proporci¨®n), que las distancias entre distintos puntos en el plano sean proporcionales a las de la esfera (tambi¨¦n con la misma proporci¨®n) y que los ¨¢ngulos entre distintas rectas en el plano sean los mismos que los ¨¢ngulos que forman las l¨ªneas correspondientes en la esfera.

Las proyecciones m¨¢s utilizadas para la realizaci¨®n de mapas presentan alguna de estas caracter¨ªsticas, pero fallan en otras. El problema es que es imposible construir un mapa plano de la Tierra que cumpla esos tres requisitos. Y este hecho no es muy dif¨ªcil de comprobar.

En una esfera podemos dibujar un tri¨¢ngulo de una manera parecida a como lo har¨ªamos en un folio. Nosotros vamos a representar un tri¨¢ngulo muy especial:

Nos situamos en el punto m¨¢s alto de la esfera (que podr¨ªamos llamar polo norte) y bajamos hasta el ecuador de la misma mediante un arco de circunferencia. Volvemos a situarnos en el polo norte, giramos 90? desde el arco dibujado antes y volvemos a bajar al ecuador con otro arco de circunferencia. Y ahora unimos los dos puntos del ecuador mediante otro arco de circunferencia. Nos queda un tri¨¢ngulo esf¨¦rico que, adem¨¢s, tiene la caracter¨ªstica de que sus tres ¨¢ngulos miden 90?:

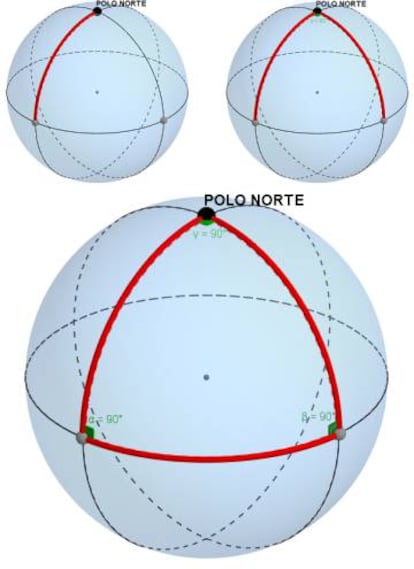
Si quisi¨¦ramos construir un mapa plano perfecto proyectando esta esfera, dicho tri¨¢ngulo esf¨¦rico deber¨ªa convertirse en un tri¨¢ngulo plano, un tri¨¢ngulo de los de toda la vida. Pero, como muchos habr¨¦is apreciado ya, eso es imposible, ya que la suma de los ¨¢ngulos del tri¨¢ngulo esf¨¦rico es 270? y la suma de los ¨¢ngulos de un tri¨¢ngulo plano debe ser, obligatoriamente, 180?. Por tanto, no se puede proyectar de manera perfecta una esfera sobre un plano y, en consecuencia, la construcci¨®n de un mapa plano perfecto de la Tierra es imposible.

El ejemplo del tri¨¢ngulo esf¨¦rico nos ha servido para descartar que pueda construirse un mapa plano perfecto de nuestro planeta, pero se puede profundizar algo m¨¢s en las matem¨¢ticas que hay detr¨¢s de este hecho. Una proyecci¨®n que nos diera como resultado un mapa plano perfecto se denomina isometr¨ªa. Por otra parte, para cada punto de una superficie se puede dar una medida de c¨®mo se curva dicha superficie denominada curvatura de Gauss.

El propio Gauss demostr¨® que la curvatura que lleva su nombre se conserva mediante isometr¨ªas. Es decir, si dos superficies son isom¨¦tricas (esto es, existe una isometr¨ªa que transforma una en la otra), entonces las curvaturas de Gauss deben ser obligatoriamente iguales. Y se da la circunstancia de que la curvatura de Gauss de un plano es 0 y la de una esfera es 1 entre su radio al cuadrado, por lo que nunca ser¨¢ 0. Curvaturas de Gauss distintas implican, por tanto, que las superficies no son isom¨¦tricas. Adi¨®s a nuestro mapa perfecto.